Discrepancy between minROPP and LevMarq minimisers

[Ian Culverwell]

ROPP5 testing has shown large differences in retrievals using these two minimisers (eg see #232).

Huw Lewis documented similar differences (if not quite as bad) in GSR 6.

We should find out why minROPP and LevMarq differ.

First thoughts

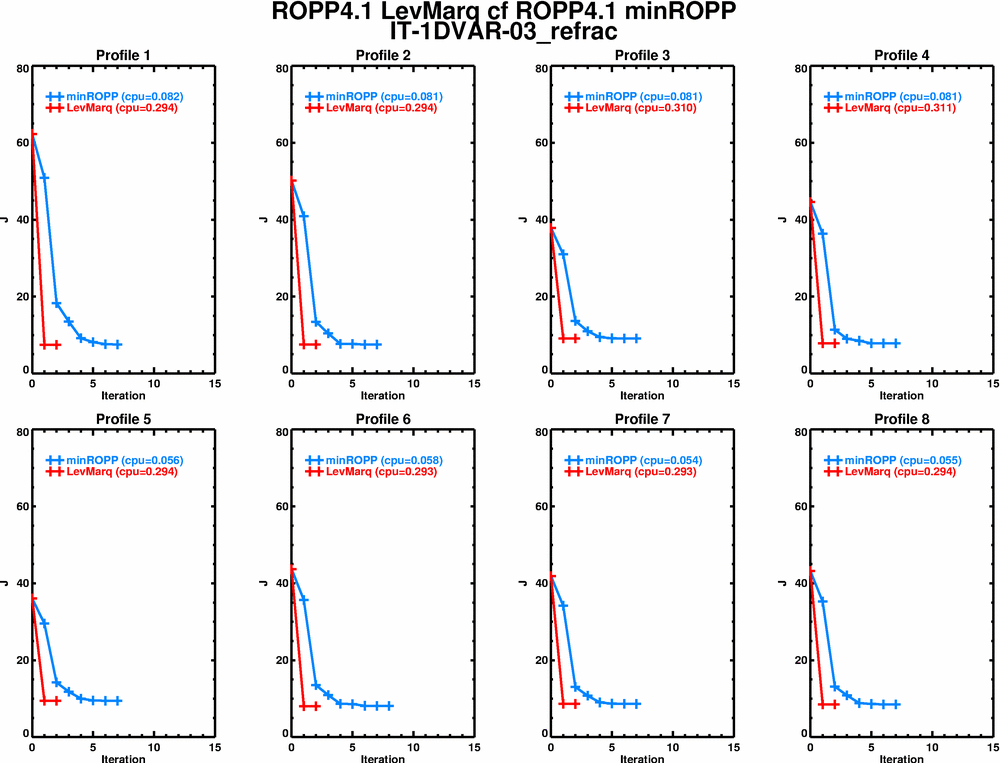
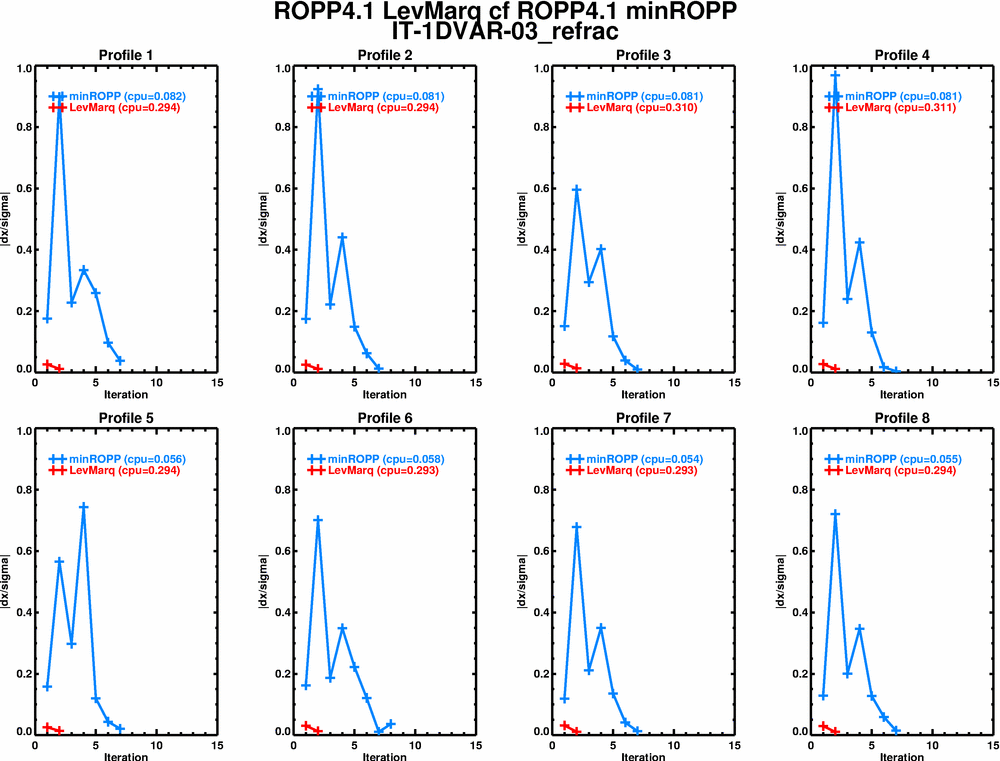
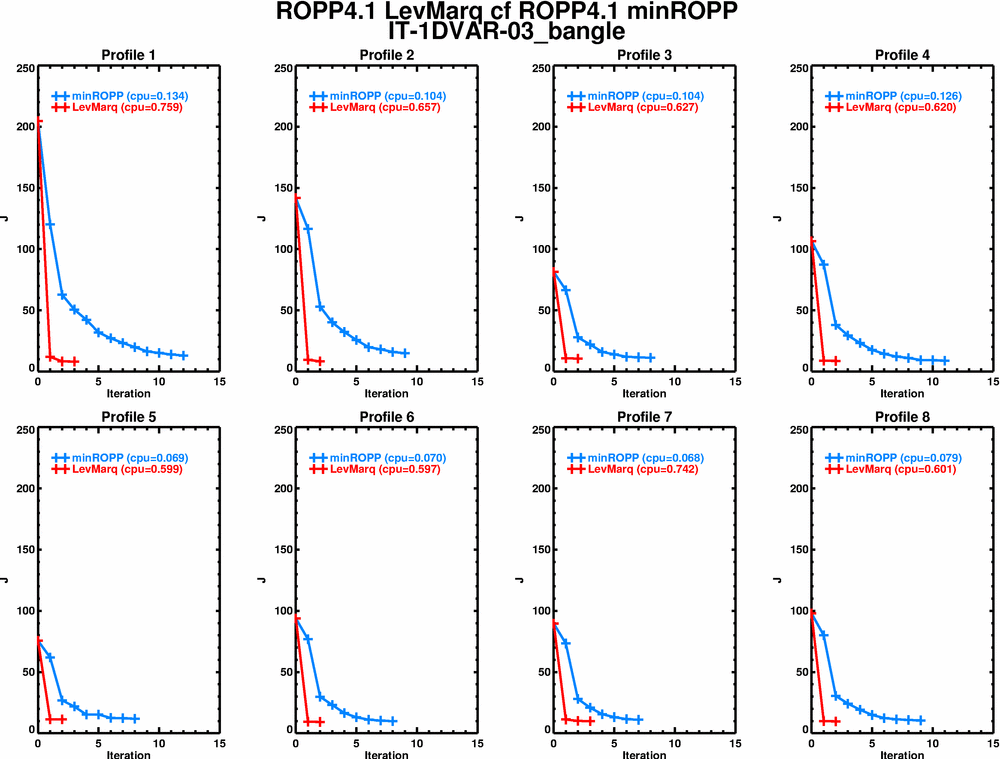
Plots of the convergence of both schemes (in terms of J and dx, the normalised change in the state from one iteration to the next) are listed below, for the 8 profiles in IT-1DVAR-03, for reference with Huw's earlier work in GSR-03 and GSR-06.

Refrac, J

Refrac, |dx|

Bangle, J

Bangle, |dx|

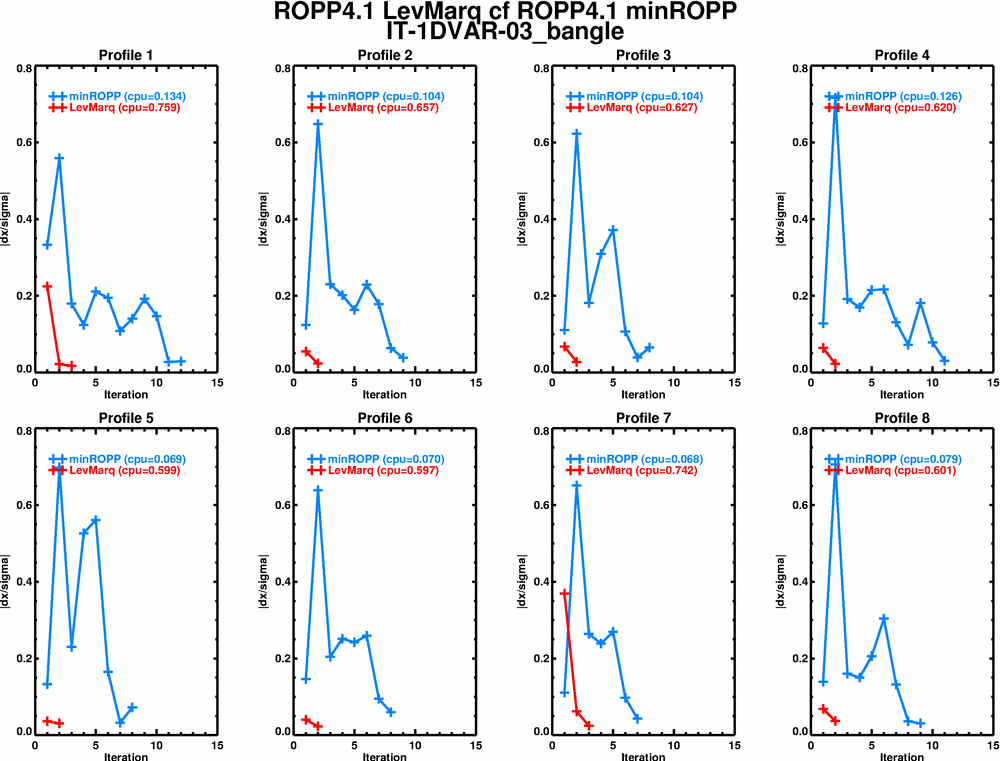
These don't really make sense to me. The change in the state is about the same for the last two steps of LevMarq, yet it has almost converged by the first of these. Is it going around the minimum or over it? (This is with the Linf (= max) norm; what does L2 say?) minROPP, on the other hand, seems to spiral in to the min.

All the cpu times (sec) for the 8 profiles in IT-1DVAR-03 are 3-4 times quicker than Huw found (linux upgrade?), but the story is the same: LevMarq converges monotonically in a few, costly, iterations, while minROPP goes all over the place before converging - quickly.

So, although minROPP converges much more slowly than LevMarq, typically needing ~5 times as many iterations, because it calculates each iteration so much more cheaply, it's around 3-5 times quicker overall.

Here are some plots of x and H(x) for each iteration of the convergence of profile 3:

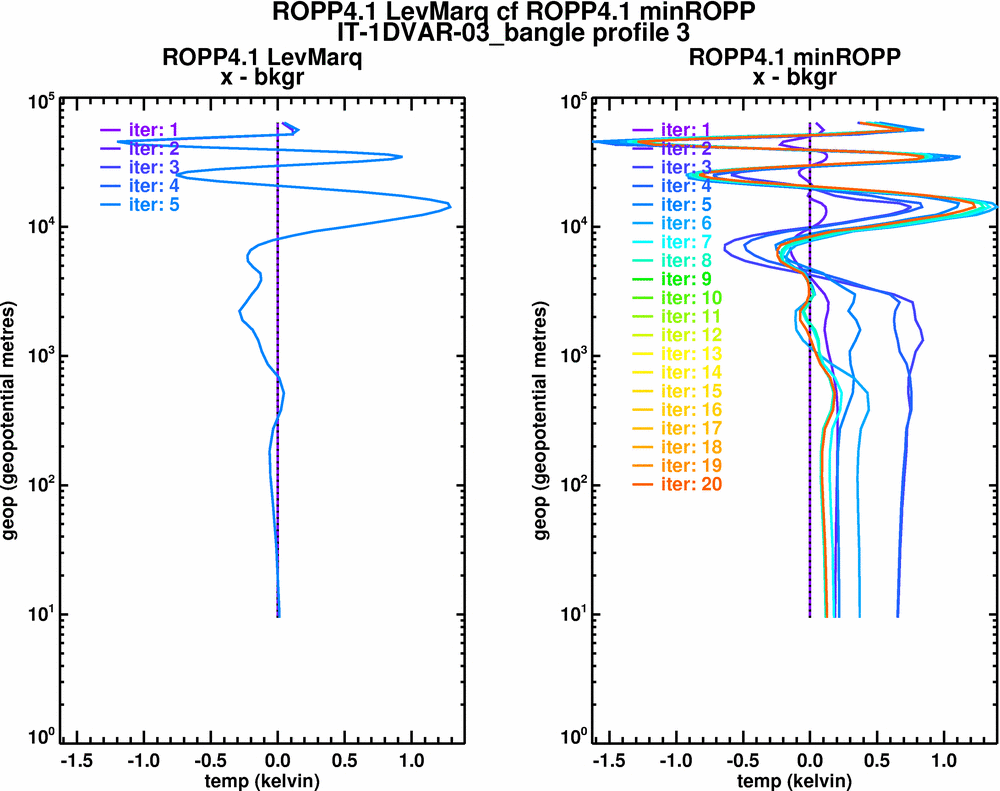
Temp - bkgr

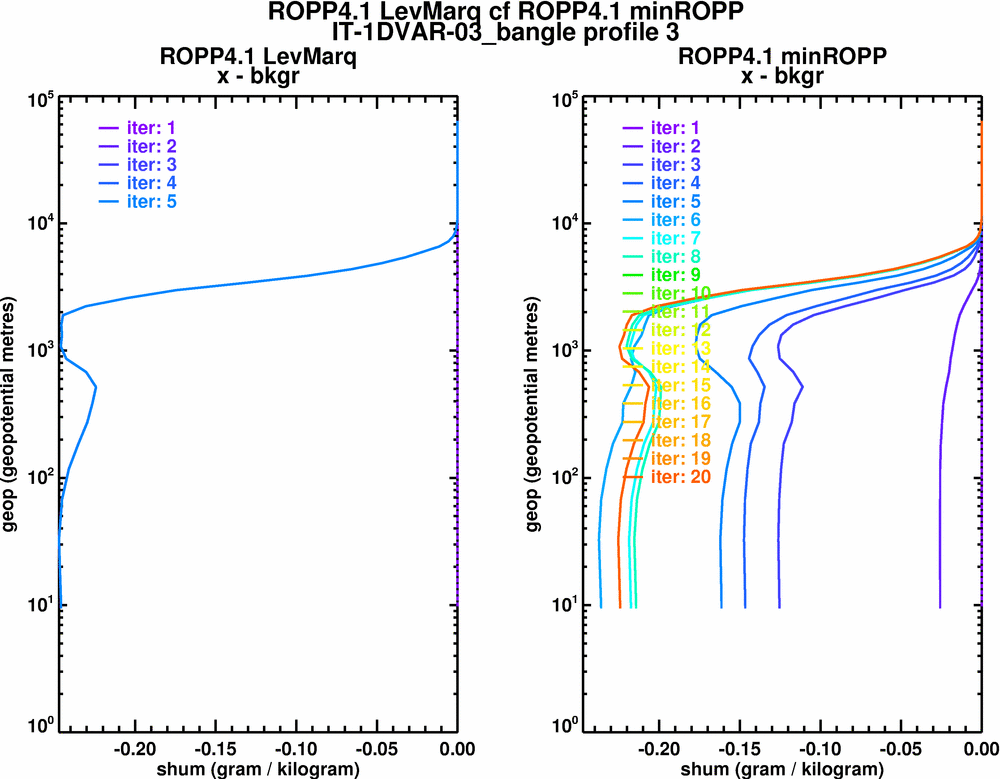
Hum - bkgr

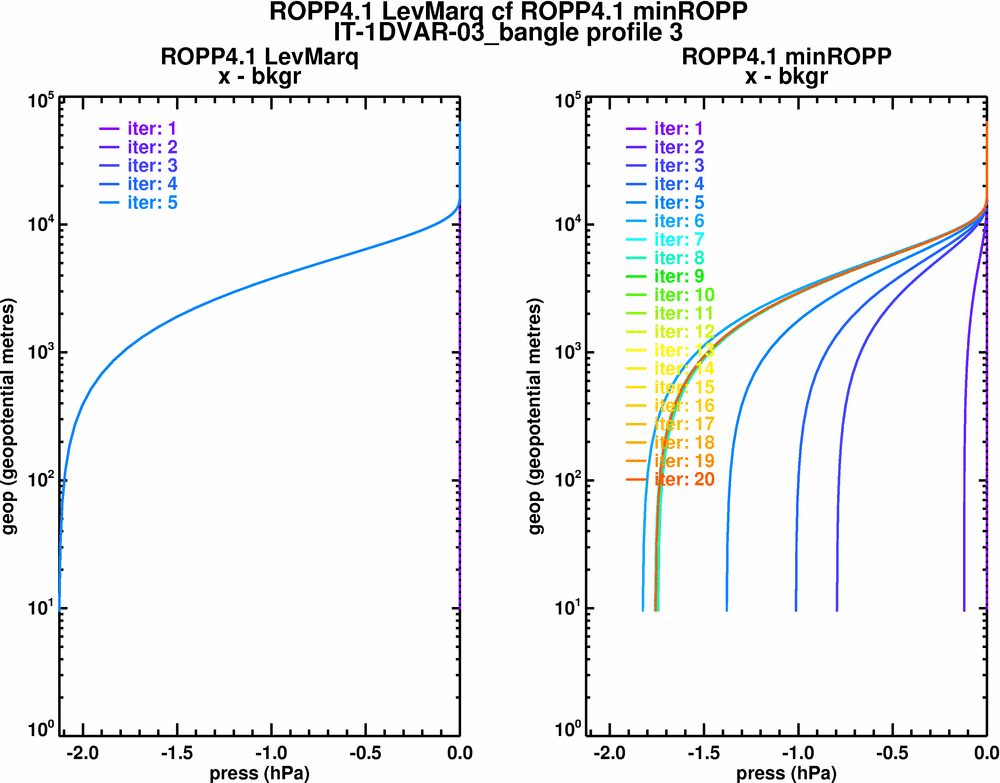
Pres - bkgr

Forward modelled Bangle - obs

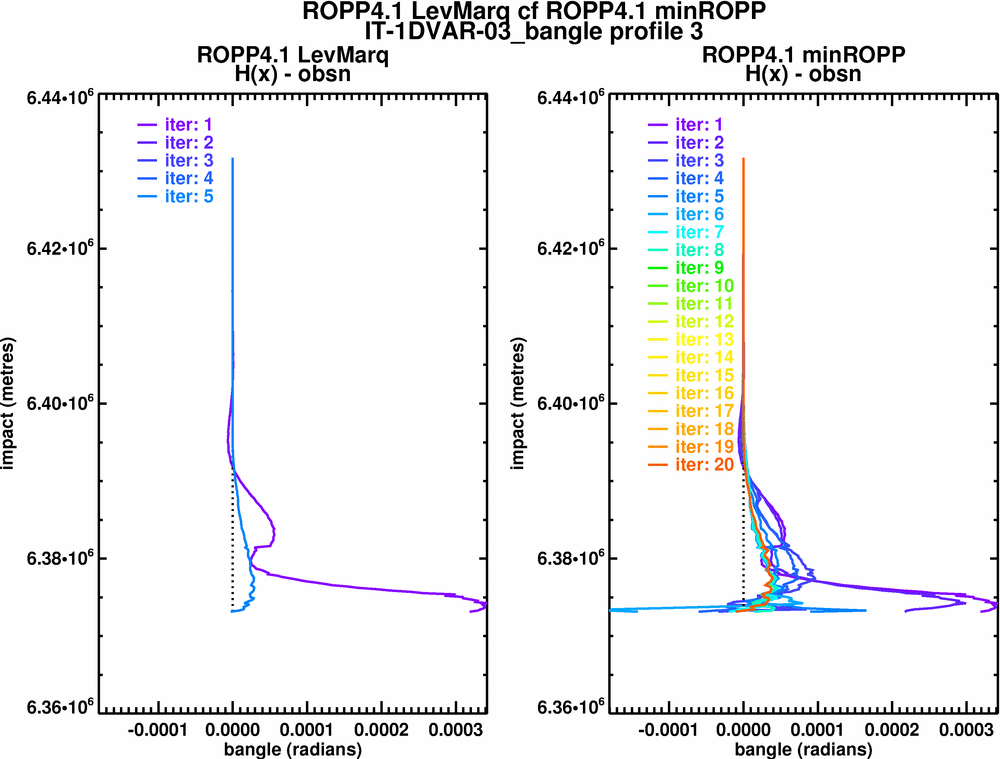
Certainly it looks as though LevMarq is doing a better job, but can we prove it? Given its extra cost, the question needs answering. I think we could try using a profile with an analytical solution (eg exponentially decaying T & q, on diff scales perhaps), roughed up with some random noise (of known statistics). Then we could see whether minROPP or LevMarq is better.

[Ian Culverwell]

Carried over to ROPP7.0 - long-term issue.