Opened 13 years ago
Closed 12 years ago
#301 closed defect (fixed)
xlf95 difference from ifort12 (et al) on IT-PP-05
| Reported by: | Ian Culverwell | Owned by: | Ian Culverwell |
|---|---|---|---|
| Priority: | normal | Milestone: | 7.0 |
| Component: | ropp_pp | Version: | 6.0 |
| Keywords: | Cc: |
Description
Following the replacement of the OCC-derived ropp_pp reference files with those from ROPP6.0, a discrepancy has come to light between the results of IT-PP-05 when ROPP is compiled with xlf95 (running under AIX on an IBM supercomputer) and when it is compiled with ifort12 and all the other compilers running on a linux box.
Investigations show that this discrepancy has been there as long as we have been testing xlf95, but that previously it was masked by the much larger difference between ROPP (built with any compiler) and OCC.
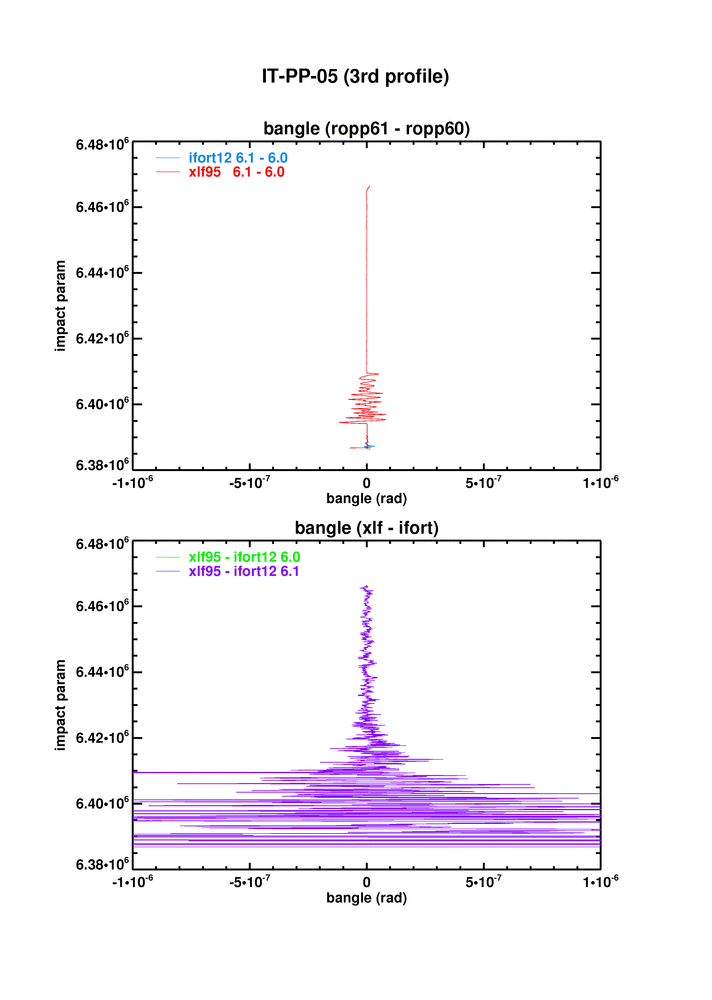
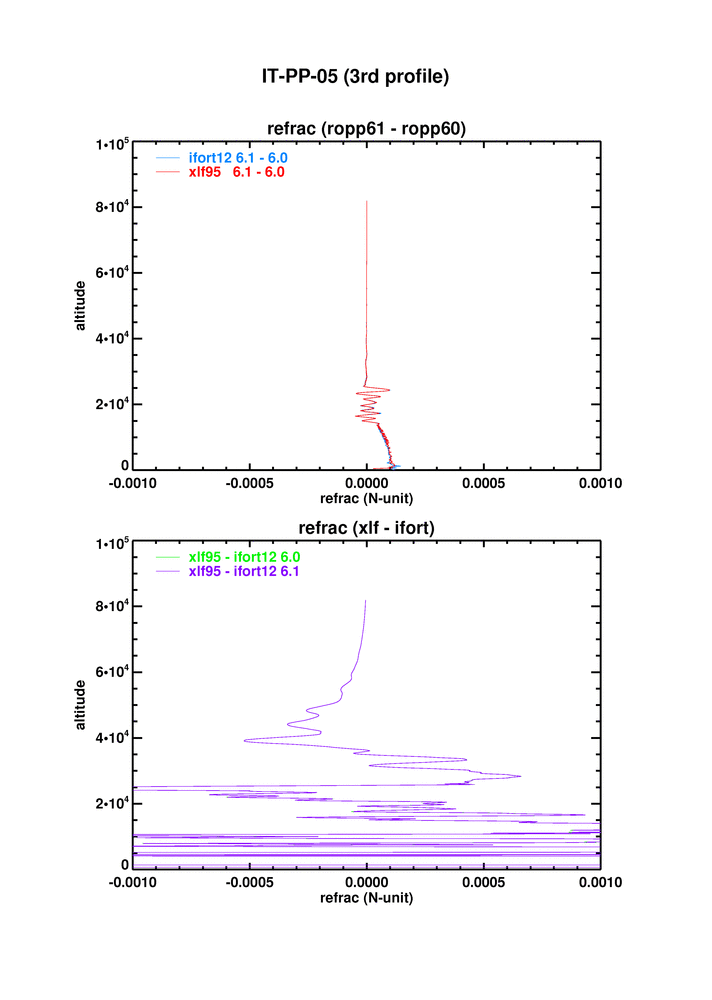
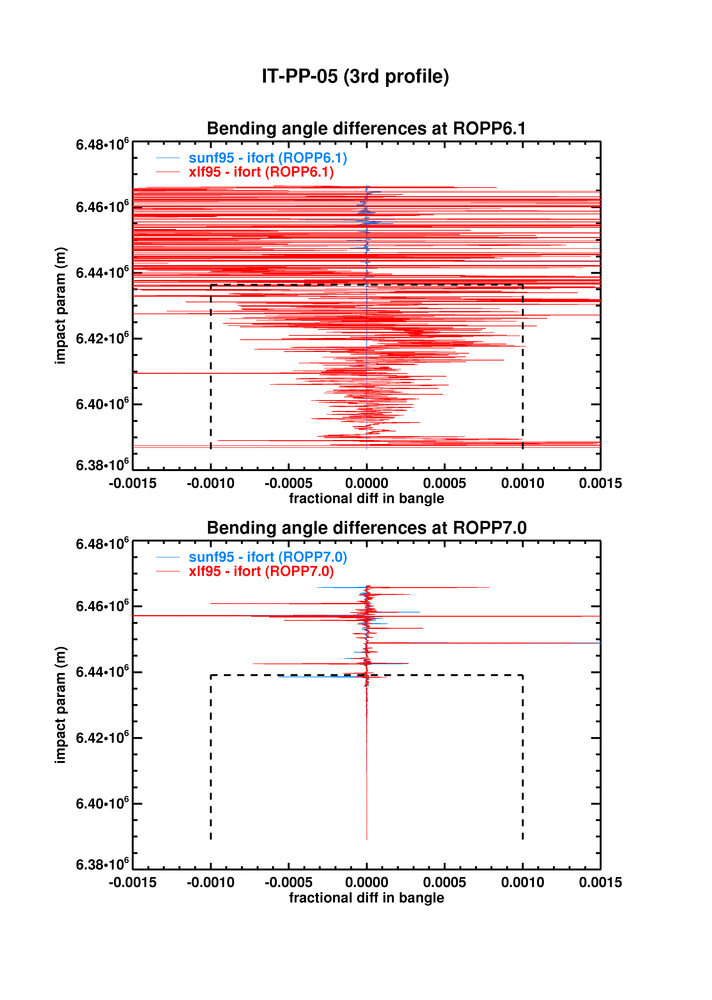
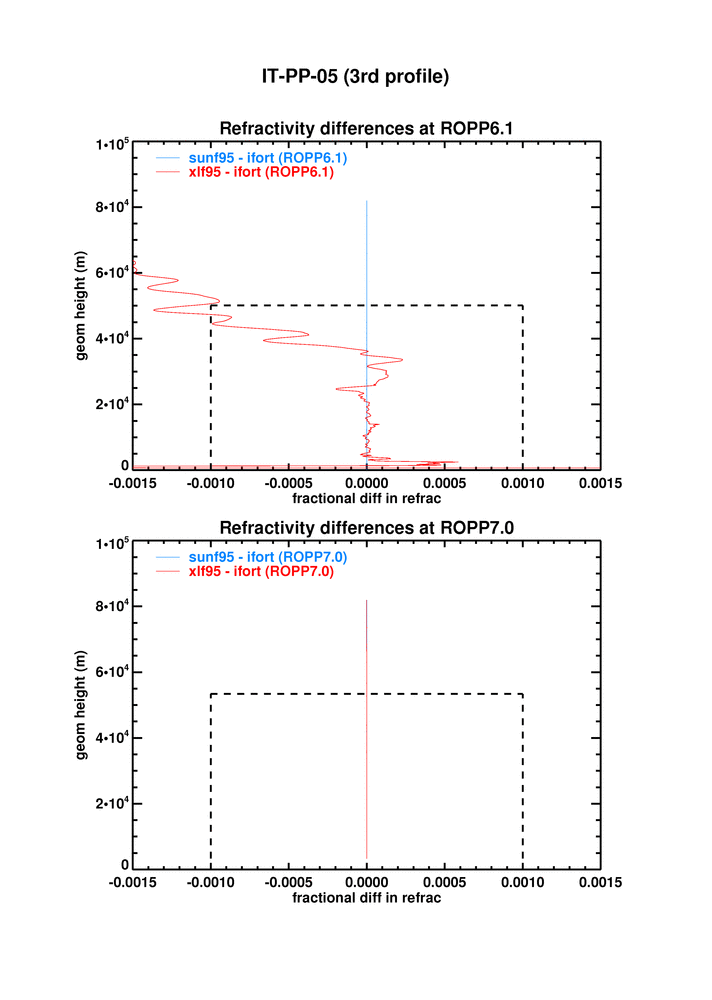
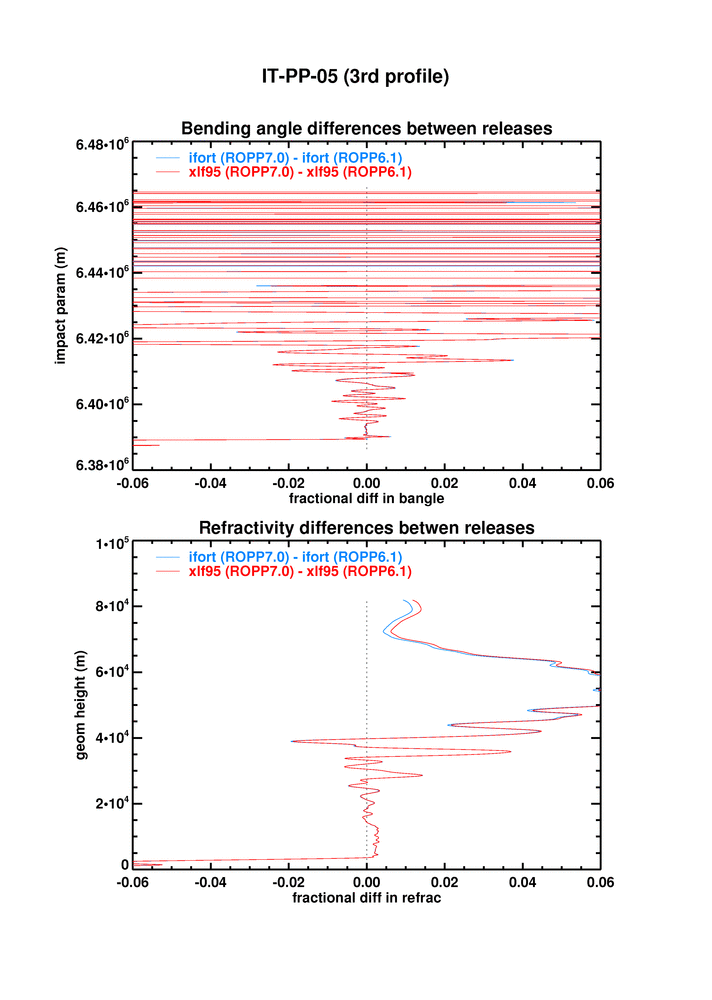
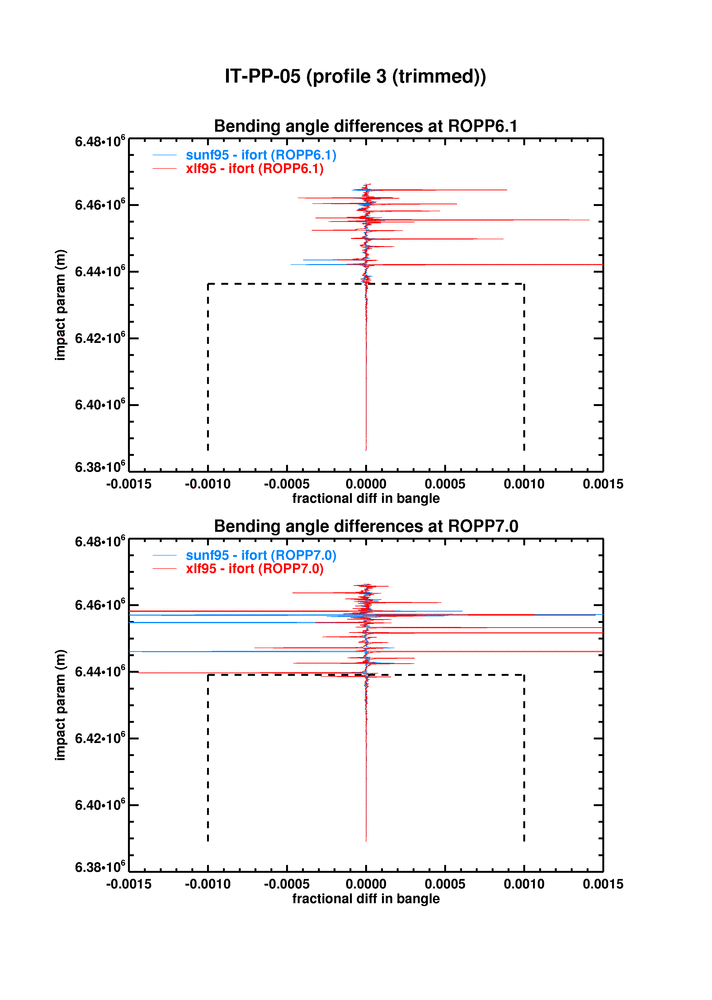
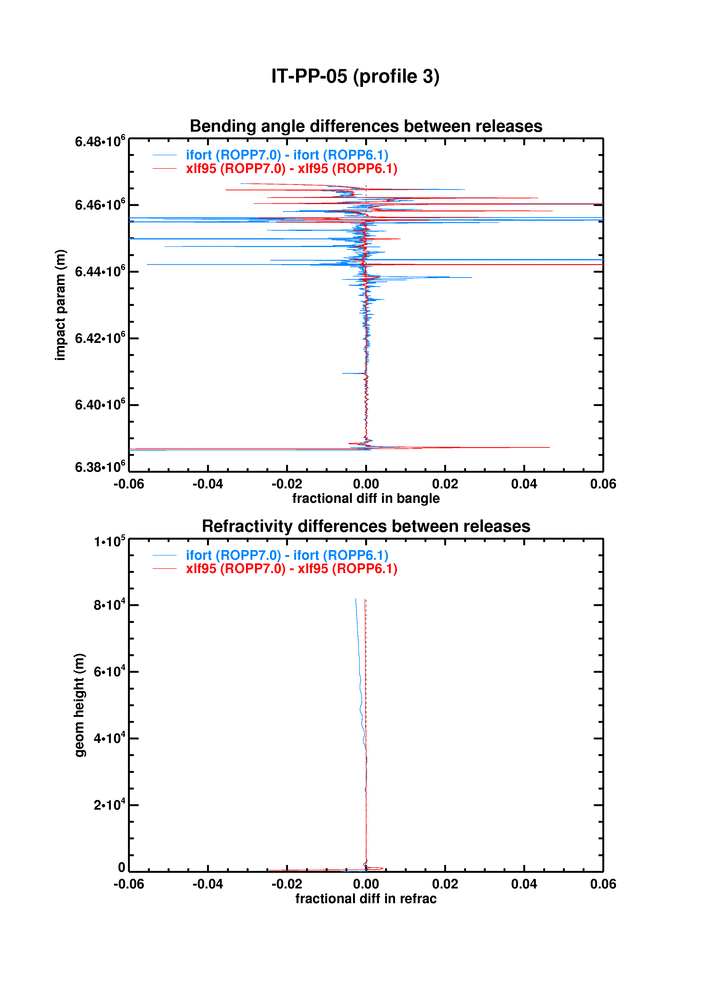
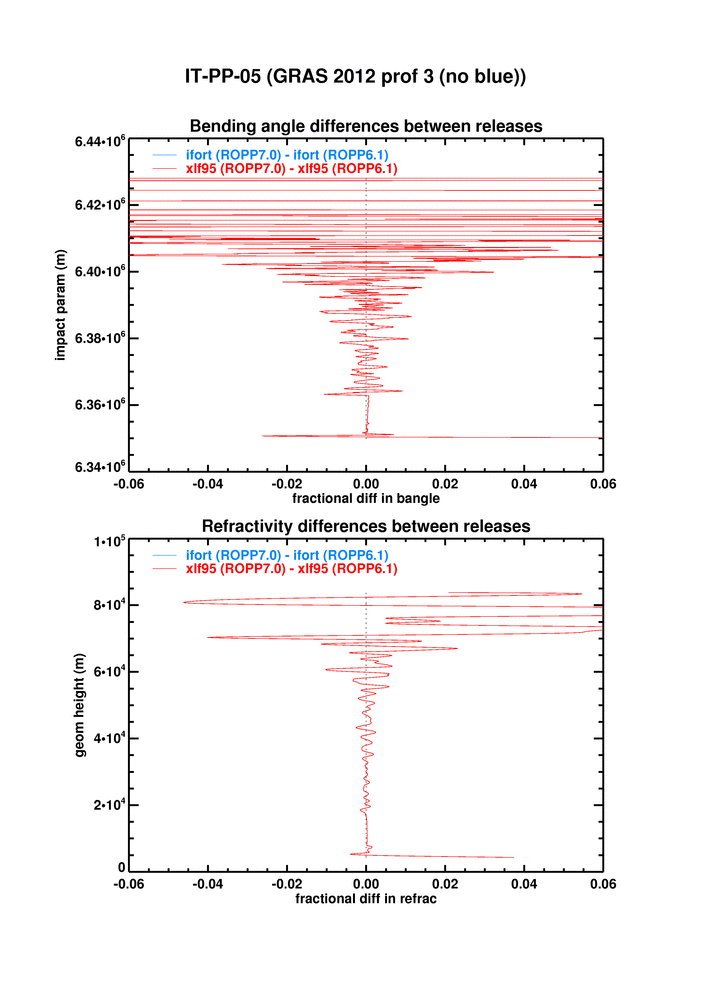
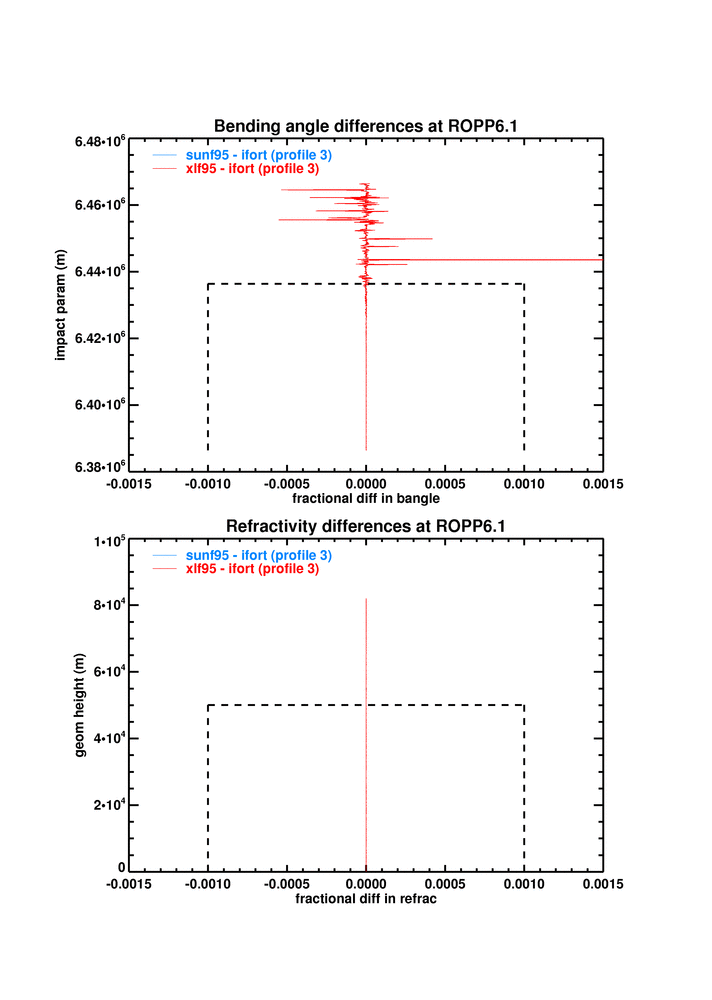
IT-PP-05 tests the ropp_pp_occ_tool on open and closed loop GRAS data. The figure below shows the differences between xlf95 and ifort, and between ROPP6.0 and 6.1, on the third profile of the test dataset, where the differences are largest.
It is clear that the difference in bangle between xlf95 and ifort12 is pretty much the same at 6.1 as it was 6.0, because the 6.0-to-6.1 change is very small. (Offline tests indicate that this small difference is largely due to a change in ropp_pp_fourier_filter.f90 made at 6.1 (see #299).)
The same is true for refractivity.
Painstaking investigations have yet to discover the reason for the difference between xlf95 and ifort12 (etc) on this dataset. It may be down to a deep-rooted difference in the performance of fortran intrinsics on the two compilers/platforms. We propose "parking" the issue for the moment, as it is delaying the release of ROPP6.1.
Attachments (27)
Change history (43)
by , 13 years ago
| Attachment: | test2_bangle.gif added |
|---|
comment:2 by , 13 years ago
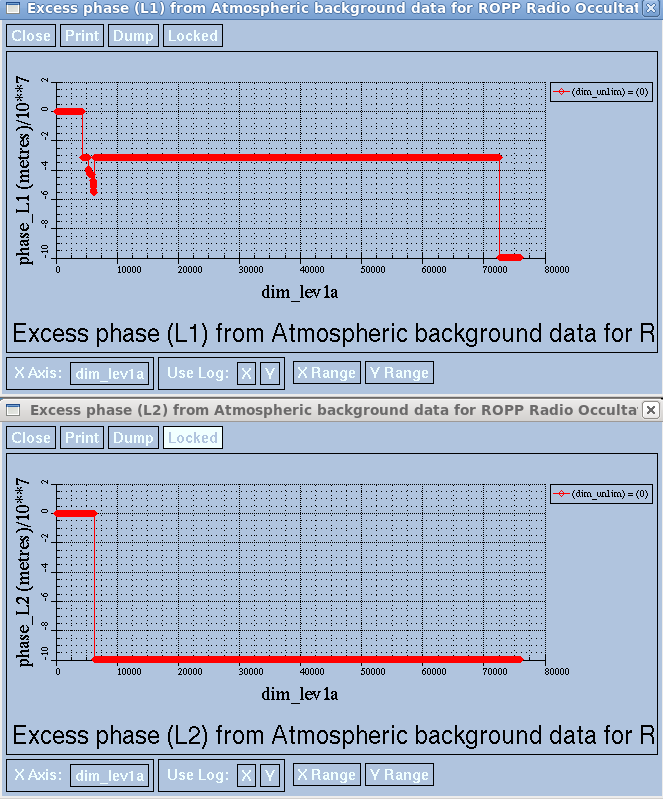
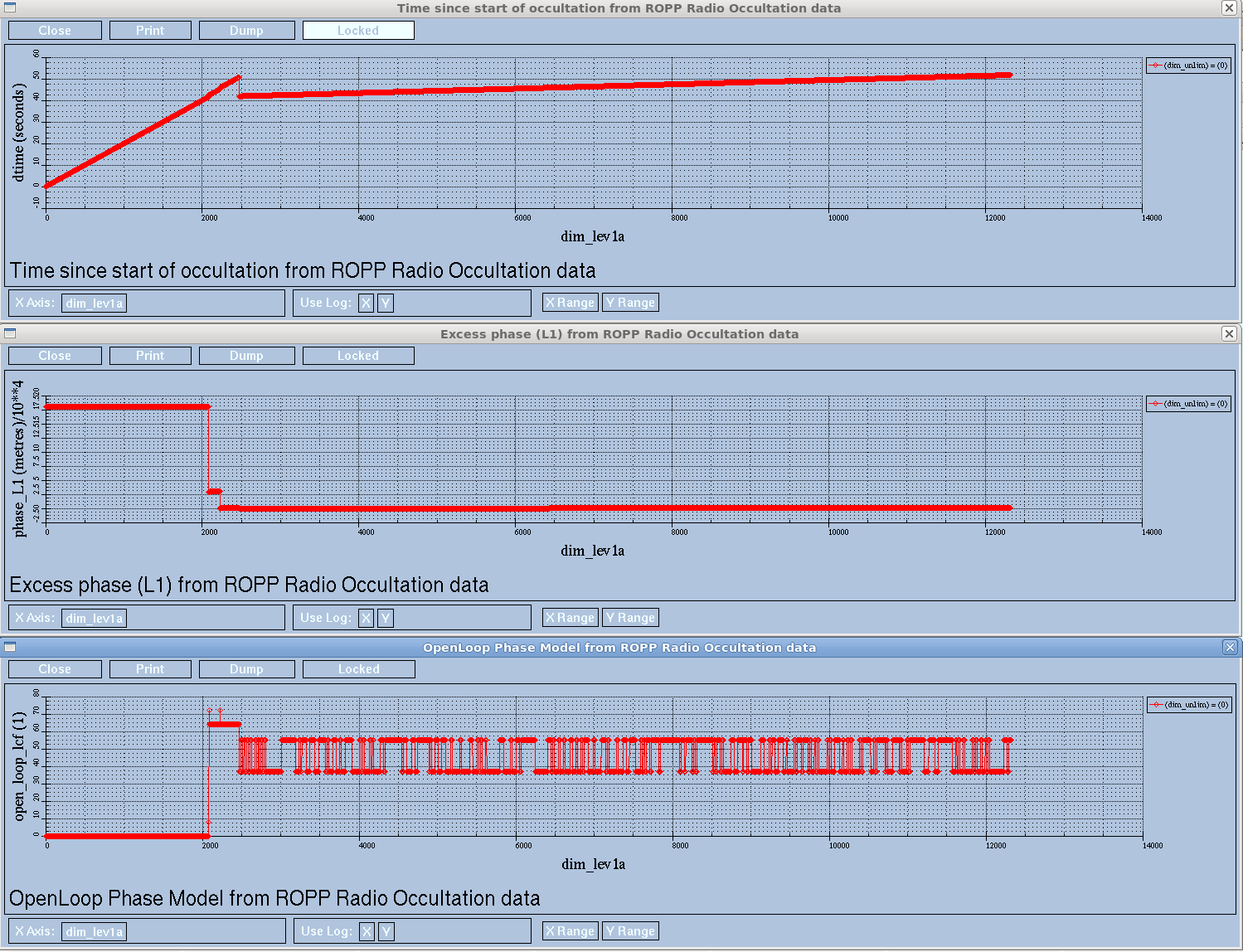
This root of this problem appears to be a data issue rather than a coding one. There are lots of rubbish phase_L1 points in the data:
Lots of phase_L1s are about -31e6, which is not ropp_MDFV (=-99999000.), and which are therefore currently processed by ropp_pp_preprocessing_grasrs.f90. This can't be right. (There are also a lot of phase_L1 values of 9.9692100e+36 at the end of the occultation, which is NC_FILL_DOUBLE, the default netCDF FillValue. These are not shown above.)
The phase_L2s are better: valid or ropp_MDFV or NC_FILL_DOUBLE (again, the latter aren't shown).
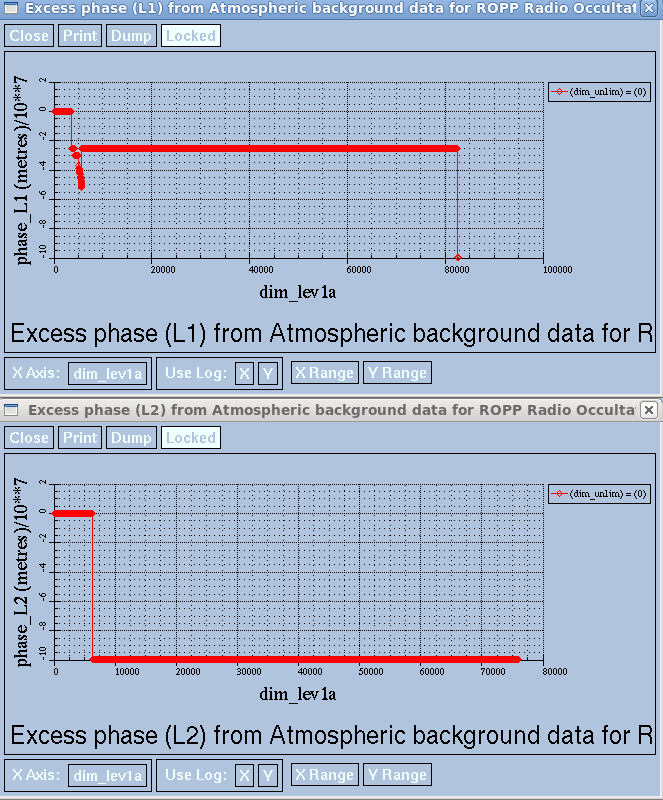
However, the same is true of the other profiles in the file, eg profile1:
This profile causes no difficulty for ROPP. We therefore assume that for profile 3 - the one that shows a significant difference betwen xlf95 and the other compilers - the amount or intensity of "bad" data is enough to throw the sensitive calculations of bending angle (and thence refractivity) into slightly different places when compiled with different compilers. Certainly the simple trick of replacing
WHERE(ro_data%Lev1a%phase_L1(:) == ropp_MDFV) WHERE(ro_data%Lev1a%phase_L2(:) == ropp_MDFV)
by
WHERE(ro_data%Lev1a%phase_L1(:) < ropp_MDTV) WHERE(ro_data%Lev1a%phase_L2(:) < ropp_MDTV)
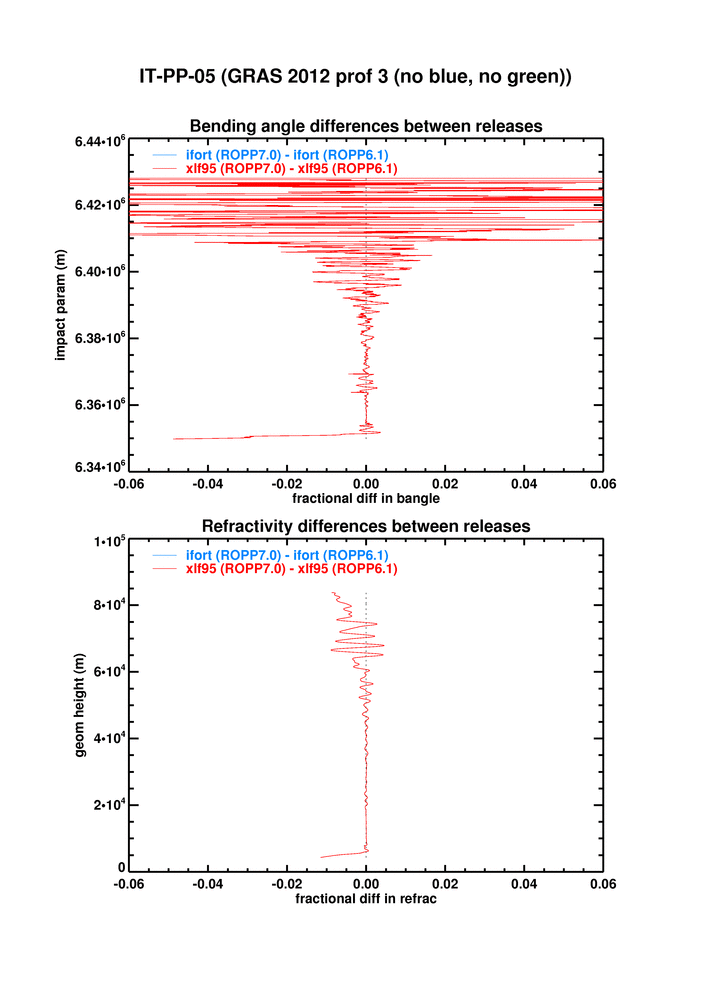
(twice) in ropp_pp_preprocessing_grasrs.f90, which omits all the dodgy stuff, seems to fix the problem. It changes the xlf95-ifort bending angle differences shown in top panel here to the ones shown in the bottom panel.
(The dashed box shows the criterion for passing the test Folder test: |diff| < 0.1% in lowest 50km.)
Similarly for the refractivities:
Job done? I don't know. Removing all this bad data has a big (~5%) difference on the derived bending angles and refractivities:
Is this acceptable? Maybe a better question is: are the original bangle and refrac profiles, partly based on phase_L1s ~ -31e6, acceptable? And we still don't really know why the dodgy data provoked a difference on xlf95. I suggest we leave this ticket open, and discuss at the DRI.
I don't know how or why these rubbish phases get into the input dataset. Note that the whole issue of the treatment of "bad" data in ropp_pp input files is discussed in ticket #287.
(In passing, I note that the results of the Global MSIS search: Month = 11 Lat = 60. Lon = 340., seem to be completely wrong for this profile, which has month[0]=9, lat[0]=-46.2301, lon[0]=-54.9948. This issue is highlighted in ticket #317.)
by , 13 years ago
| Attachment: | IT-PP-05_prof3_dtime_phase_Li_open_llop_lcf.png added |
|---|
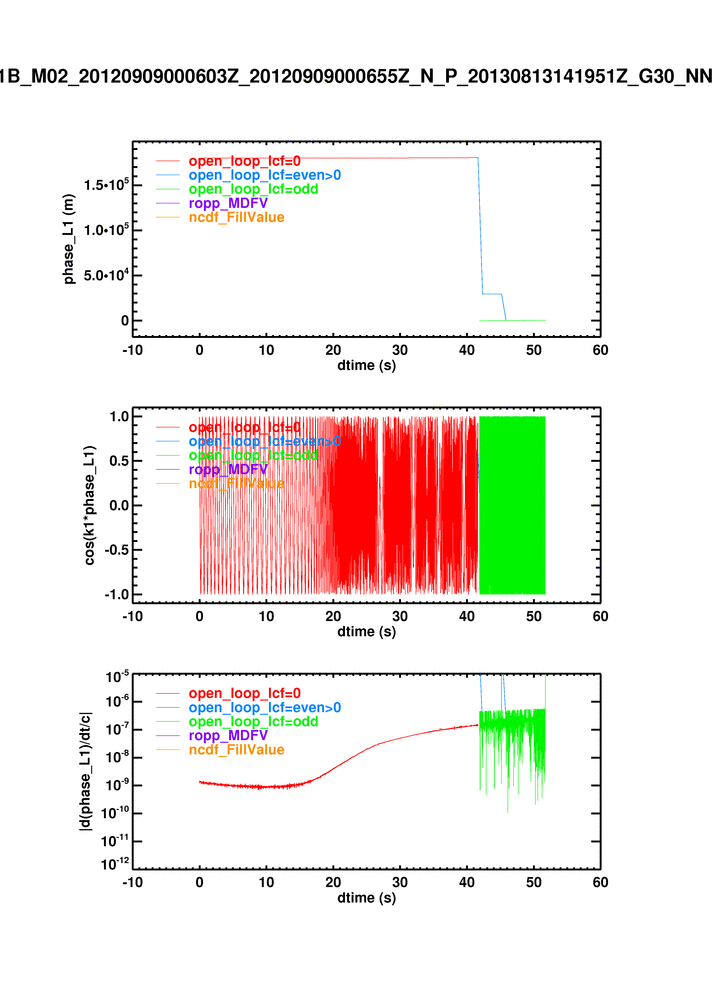
IT-PP-05_prof3_dtime_phase_Li_open_llop_lcf.png
comment:3 by , 13 years ago
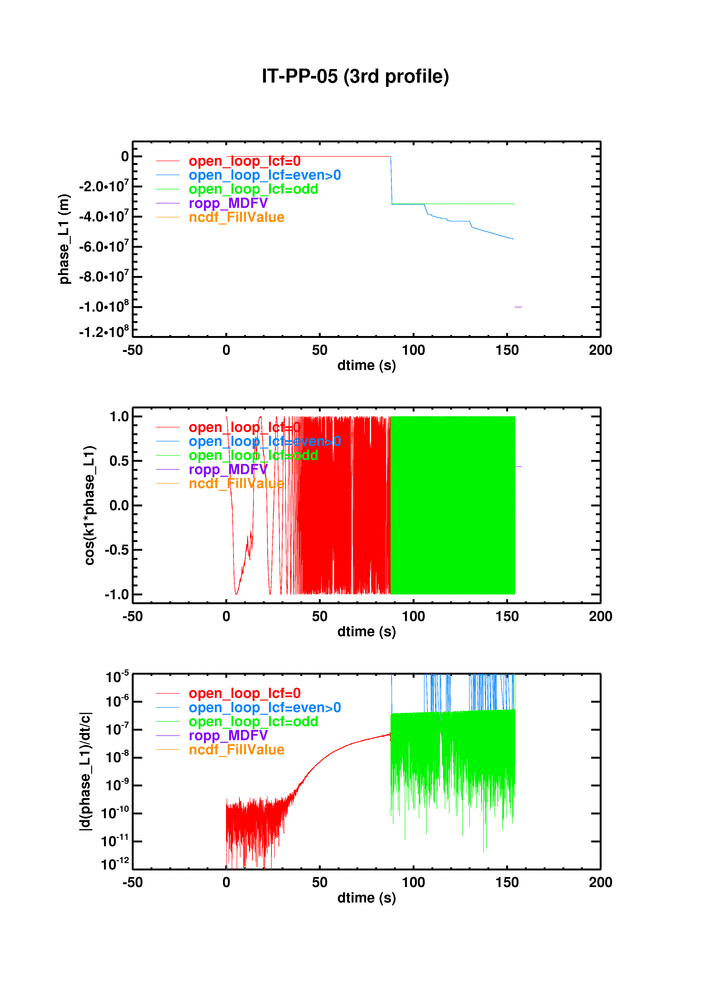
Discussed with Stig: perhaps the phase=-31e6 is OK. It's only the derivative that matters, and this could just be raw sampling data. See the open_loop_lcf flag:
[[Image(IT-PP-05_prof3_dtime_phase_Li_open_llop_lcf.png)]
Break down phase_L1 into regions defined by this flag:
[[Image(phase_L1.gif)]
It appears to be the blue region (open_loop_lcf = even > 0) that's causing the trouble - phases all over the place. When I omit this section of data, and rerun in the old code ()the blue and the green are omitted in the new code), I see no significant difference between the xlf95 and ifort:
[[Image(test3_1.gif)]
(Sim for refrac).
comment:4 by , 13 years ago
comment:5 by , 13 years ago
comment:6 by , 13 years ago
If this works on old and new data, then a reasonably simple fix is to replace
icl_min = SUM(MINLOC(ro_data%lev1a%dtime(:), MASK = .NOT. BTEST(LCF(:),0))) icl_max = SUM(MAXLOC(ro_data%lev1a%dtime(:), MASK = .NOT. BTEST(LCF(:),0)))
with
icl_min = SUM(MINLOC(ro_data%lev1a%dtime(:), MASK = LCF(:)==0) icl_max = SUM(MAXLOC(ro_data%lev1a%dtime(:), MASK = LCF(:)==0)
in ropp_pp_preprocess_grasrs.f90. By this means we are defining the open loop region as the one in which LCF is 0, not just even.
But it remains to be seen what happens when new data are passed through the routines.
comment:7 by , 13 years ago
Axel von Engeln kindly provided, via Yago Andres and Chris Burrows, 5 recent (2012) level 1a phase datasets from EUMETSAT, in grouped netCDF4 format. After converting to standard ROPP format by using eum2ropp, the resulting profiles were run through IT-PP-05 on ifort (on a linux box), sunf95 (on a linux box), and xlf95 (on the HPC).
Result: no significant (ie > 0.1% fractional difference in 0-50km) difference between any of them.
This is good - it means that a new test dataset using these profiles should pass the test folder. (We already know it passes the xlf95 test.)
Bt we don't really know why. The new profiles still overlapping open loop and raw sampling sections. Then again, four of the 5 old (2007) profiles had that, and they passed the test. One clue: the L1 phases in the overlap region tend to be quite small (~1-1e5) and positive, rather than ~ -31e6 as they were before. Perhaps it's just good luck.
comment:8 by , 13 years ago
comment:9 by , 13 years ago
comment:10 by , 13 years ago
I meant overlapping closed loop and raw sampling, of course. (Thanks, Stig!)
comment:12 by , 12 years ago
Removing the overlapping CL data from the new GRAS profiles has a significant (~few %) effect on the processed bangles and refracs:
Interestingly, this is larger than the effect of removing overlapping CL and RS data:
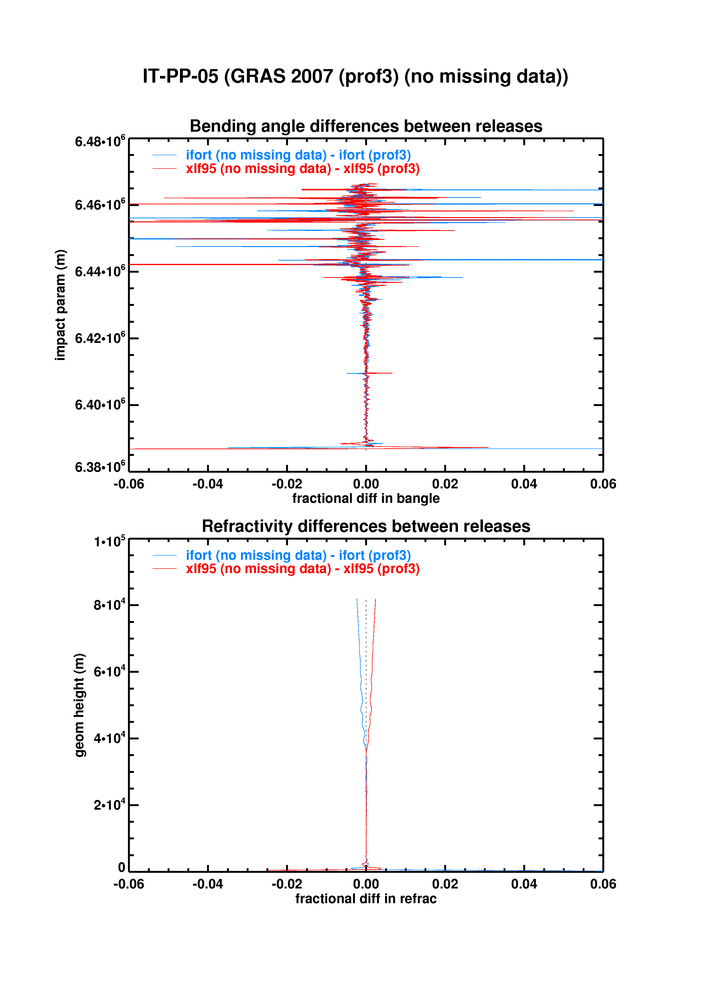
So, backpedalling a bit, removing data is probably not such a good idea. This conclusion is reinforced by the hilarious discovery that removing the missing phase_L1 data from profile 3 of the earlier 2007 GRAS RS dataset has a measurable impact on the preocessed bangles and refracs:
(Note the icing on the cake that the effect of removing missing data is different for xlf95 and ifort.)
What a load of rubbish.
I propose deferring the whole question to ROPP8.0, when hopefully someone else will look at it.
comment:13 by , 12 years ago
Stig Syndergaard (DMI) has taken a close look at this problem. His email and attachments are attached. Key points:
ropp_pp_cutoff_amplitude: There's a small bug in this, which results in (one) too many points in the merged sample. Has a small impact.
ropp_pp_preprocess_grasrs: Stig discovered that the orbit fitting (via ropp_pp_regression) uses all the data, not just the non-missing stuff. (Later processing uses properly masked data.) This explains the differences shown in the last figure above, for omitting bad data (as inferred from the value of LCF flag) from the orbit-fitting resulted in exactly the same results when run on the full and the expurgated datasets.
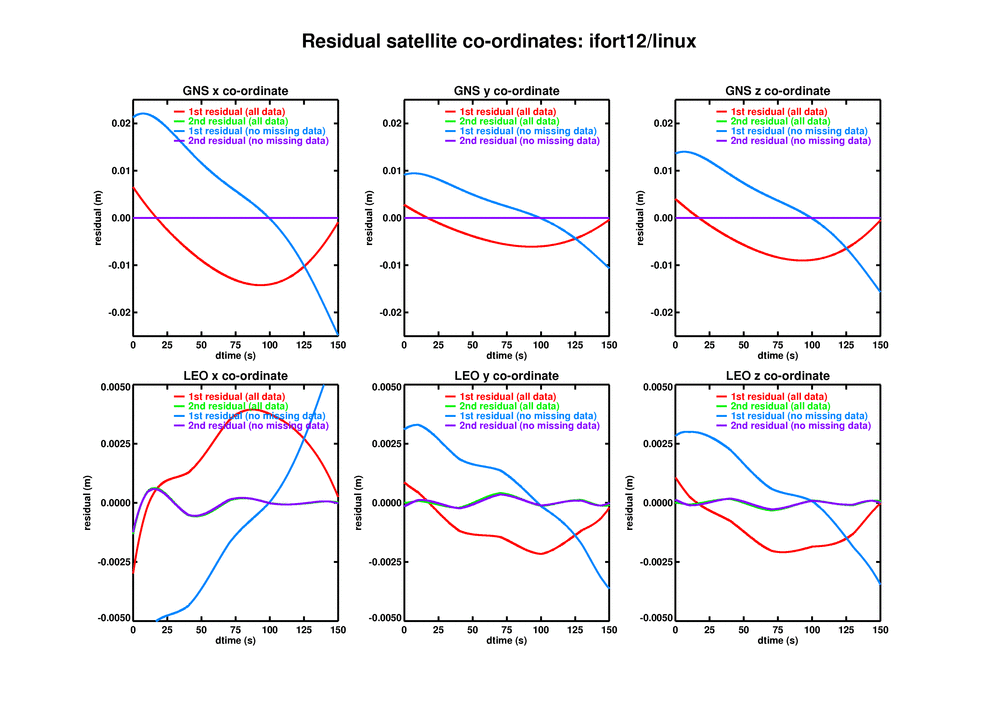
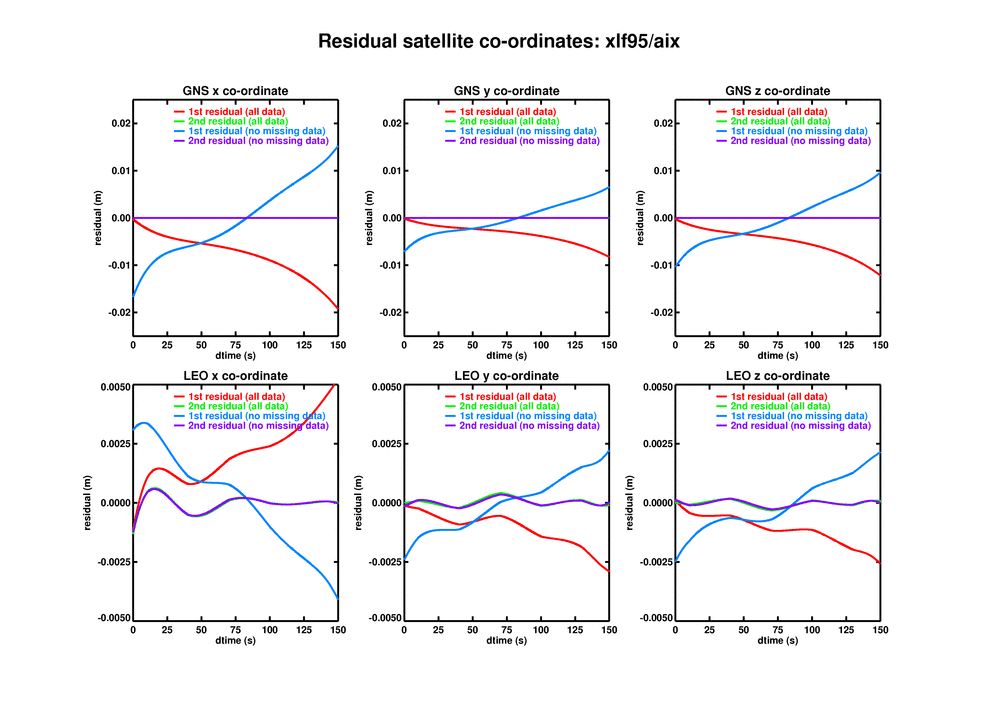
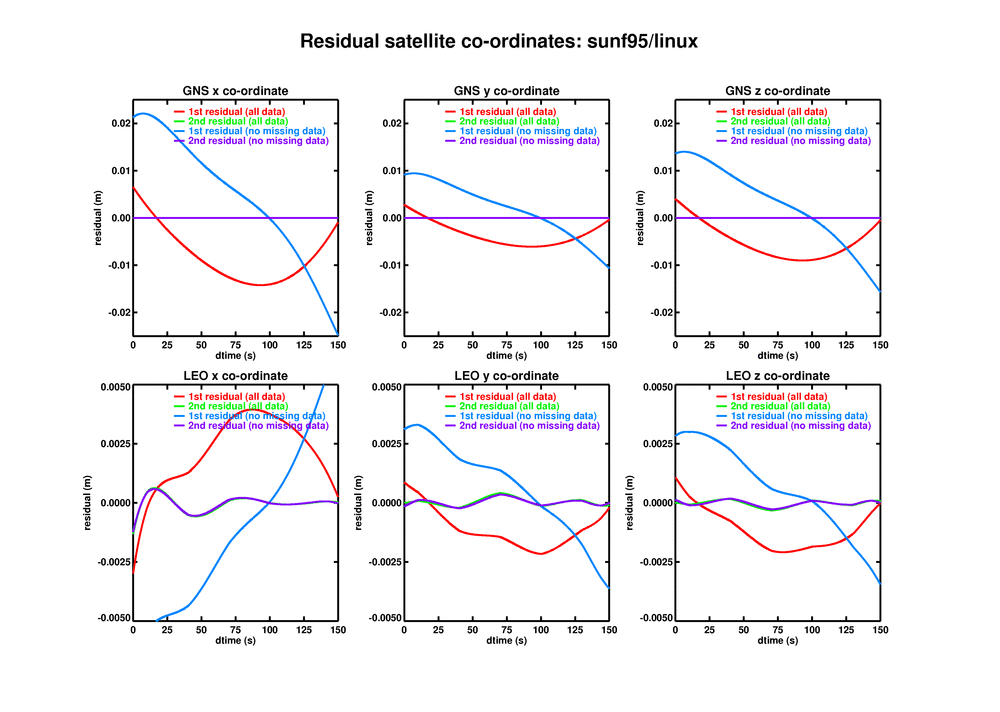
ropp_pp_residual_regression: There remains, however, the puzzling difference between the results using xlf95/HPC and ifort/linux. Stig suggested that this might be due to the numerical infelicity of the orbit-fitting routine ropp_pp_regression, which fits a 5th degree polynomial through the each of the {x, y, z} co-ordinates of the LEO and the GNSS satellite. Since these co-ordinates are almost constant during an occultation, the resulting inversion is a bit ill-conditioned. He found residuals (fit-data) of up to 2 cm ("1st residual" in the attached xgns.png). By refitting these residuals (using ropp_pp_residual_regression in ropp_pp_utils) these were much reduced ("2nd residual" in the attached xgns.png).
Stig's hunch was that this regression would likely be sensitive to the compiler/platform, and might therefore explain the xlf95/HPC and ifort/linux differences. Happily this seems to be borne out in practice.
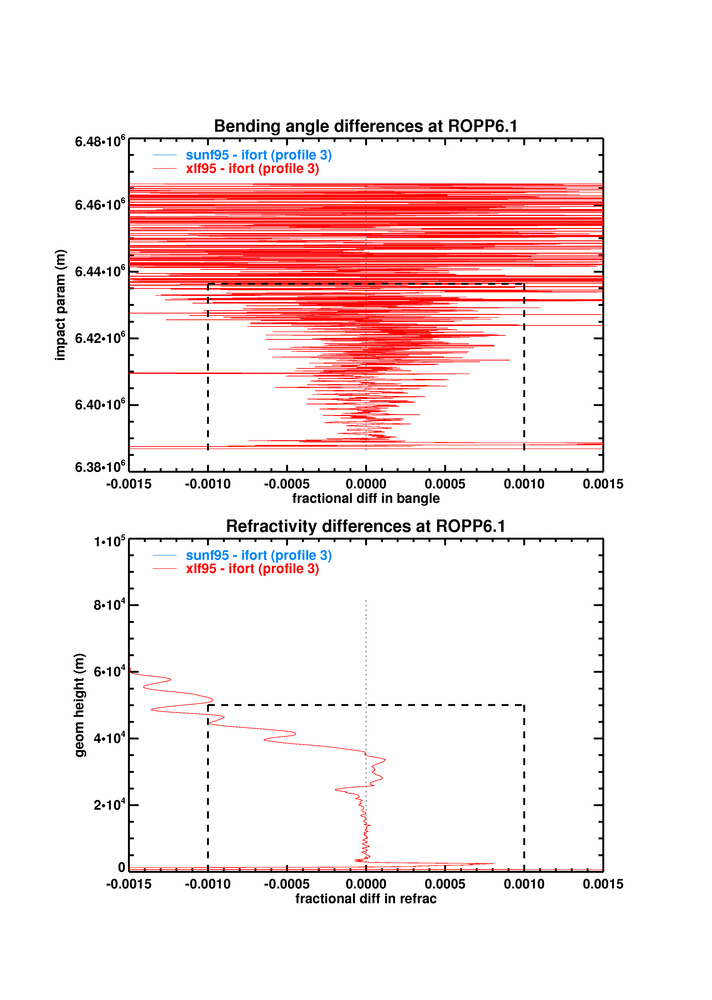
As a reminder, here are the xlf95-ifort differences in bending angle and refractivity for the original code:
These are outside the 0.1% threshold for acceptability.
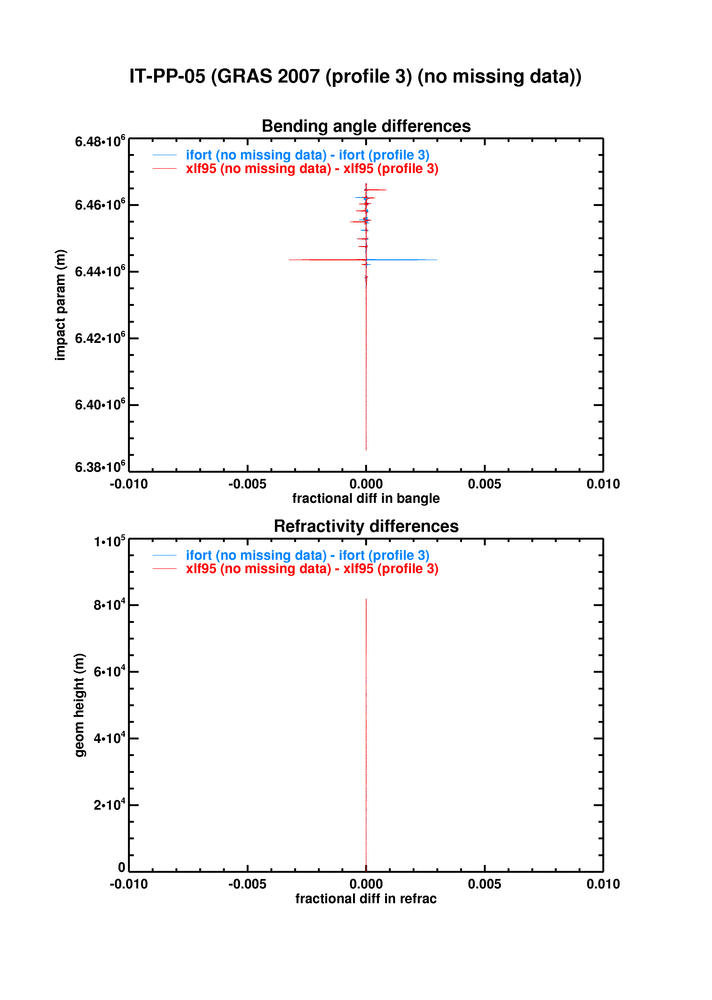
Here are the corresponding results when the regression is improved by calling ropp_pp_residual_regression on the residuals from ropp_pp_regression, and then amending the fitting coefficients accordingly:
These are within the 0.1% threshold for acceptability.
These are both for the full dataset (missing data included), which is why there remains a tiny difference between the "purple" and "nopurple" datasets:
(This difference can be removed entirely by applying the fix described in the second point above, but a general algorithm to do so on a dataset with missing raw sampling data anywhere needs a little more work.)
SUMMARY
- Differences between caused by presence (sic) of missing data explained by the fact that all the data are used in the orbit-fitting routines.
- These routines are compiler/platform sensitive, but can be made significantly less so by fitting the residuals (fit-data) from the first fit, and updating the fitting coefficients appropriately.
by , 12 years ago
| Attachment: | test3_original_p1.gif added |
|---|
comment:14 by , 12 years ago
I calculated the 1st and 2nd residuals on IT-PP-05_prof3, as Stig did, for ifort/linux:
and for xlf95/HPC:
The first residuals are very different on the two platforms, while the 2nd residuals are much smaller and much more similar. This explains the above results very neatly, and strengthens the case for regressing the residuals in the orbit calculations in ropp_pp.
comment:15 by , 12 years ago
comment:16 by , 12 years ago
| Resolution: | → fixed |
|---|---|
| Status: | new → closed |


test2_bangle.gif