Opened 7 years ago
Closed 4 years ago
#646 closed defect (fixed)
Issues with the bending angle 1dvar minimizer
| Reported by: | Ian Culverwell | Owned by: | Ian Culverwell |
|---|---|---|---|
| Priority: | major | Milestone: | 11.0 |
| Component: | ropp_1dvar | Version: | 9.0 |
| Keywords: | minROPP, Levenberg-Marquardt | Cc: | Johannes K. Nielsen, frcm |
Description
Chris Marquardt (EUM) has identified some issues with the 1dvar minimisers in ROPP. Here is what he says.
Minimiser issues in ROPP 9.0
This note reports on some results I have obtained with the vanilla bending angle 1DVar from ROPP v9.0 (and also a modified version I prepared.) In general, all runs were performed using a 1DVar configuration based on ROPP's default ecmwf_bangle_1dvar.cf. The only difference common to all tests I ran is that the covariance methods were chosen differently from the default settings, mostly because RSFC was the only method supporting ECMWF's current 137 levels (and I don't remember the reason for chosing a different observation covariance method, to be honest):
#bg_covar_method = VSFC # Variable Sigmas, Fixed Correlations
bg_covar_method = RSFC # Relative Sigmas, Fixed Correlations
#obs_covar_method = VSDC # Variable Sigmas, Diagonal Correlations
obs_covar_method = FSFC # Fixed Sigmas, Fixed Correlations
In all experiments, shown below, I use the first profile we got from Metop-C (available in the ROPP bending angle file data/eum/first.nc; that is also how I discovered the problem. The experiments described below can be carried out by running the scripts run_1dvar-00, run_1dvar-01, run_1dvar-02, run_1dvar-03, and run_1dvar-00, respectively.
MINROPP
Using MINROPP as minimiser and running this setup on the first Metop-C profile gives the following output (which can be reproduced with the configuration file ecmwf_bangle_1dvar-01.cf:
---------------------------------------------------------------------
ROPP Bending Angle 1D-Var
---------------------------------------------------------------------
INFO (from ropp_1dvar_bangle): Reading configuration file ecmwf_bangle_1dvar.cf.
INFO (from ropp_1dvar_bangle): Reading observation data for profile 1 from the file
first.nc.
INFO (from ropp_1dvar_bangle): Reading background data for profile 1 from the file
../ecmwf/2018/11/13/GRAS_1B_M03_20181113100752Z_20181113100945Z_N_C_20181113121522Z_G22_NN.fw.nc.
INFO (from ropp_qc_cutoff): 33 points rejected for being above maximum impact height of 50.0 km.
INFO (from ropp_qc_bgqc): Background quality control lets all bending angle values pass.
INFO (from ropp_1dvar_solve): Using background error covariance matrix for preconditioning.
INFO (from ropp_1dvar_cost): Using absolute decrease of cost function and relative change
of state vector as additional convergence criteria.
n_iter = 1 J = 97.039 max(relative change in state) = -
n_iter = 2 J = 79.446 max(relative change in state) = 0.42320
INFO (from ropp_1dvar_cost): Convergence assumed to be achieved as the cost function is increasing
INFO (from ropp_1dvar_cost): Minimization of cost function successfully finished (according to additional
convergence criteria). Number of required iterations: 3.
INFO (from ropp_1dvar_bangle): Writing 1DVar retrieval for profile 1 to the file
first-1dvar-default.nc.
The main point in the above log is that the iteration already stops after 2 or 3 iterations. With the LEVMARQ minimiser, however, a 1DVar for the same profile results in the following output:
---------------------------------------------------------------------
ROPP Bending Angle 1D-Var
---------------------------------------------------------------------
INFO (from ropp_1dvar_bangle): Reading configuration file ecmwf_bangle_1dvar.cf.
INFO (from ropp_1dvar_bangle): Reading observation data for profile 1 from the file
first.nc.
INFO (from ropp_1dvar_bangle): Reading background data for profile 1 from the file
../ecmwf/2018/11/13/GRAS_1B_M03_20181113100752Z_20181113100945Z_N_C_20181113121522Z_G22_NN.fw.nc.
INFO (from ropp_qc_cutoff): 33 points rejected for being above maximum impact height of 50.0 km.
INFO (from ropp_qc_bgqc): Background quality control lets all bending angle values pass.
n_iter = 1 J = 97.039 max(relative change in state) = -
n_iter = 2 J = 32.400 max(relative change in state) = 0.13905
n_iter = 3 J = 32.382 max(relative change in state) = 0.16073
n_iter = 4 J = 32.378 max(relative change in state) = 0.12803
INFO (from ropp_1dvar_levmarq): Convergence assumed to be achieved as the cost function did not change by more
than 0.10000 for the last 2 iterations.
INFO (from ropp_1dvar_bangle): Writing 1DVar retrieval for profile 1 to the file
first-1dvar-default.nc.
i.e. we get quite a different cost function compared to the achieved by MINROPP (32.4 vs 79.4) - and obviously, the MINROPP minimiser isn't even near the minimum of the cost function.
It is possible to force MINROPP to do more iterations, of course. Again running MINROPP, but this time with
conv_check_n_previous = 5 # Minimum number of iterations required
(where the default value is 2 iterations; see ecmwf_bangle_1dvar-02.cf) results in the following
INFO (from ropp_1dvar_cost): Using absolute decrease of cost function and relative change
of state vector as additional convergence criteria.
n_iter = 1 J = 97.039 max(relative change in state) = -
n_iter = 2 J = 79.446 max(relative change in state) = 0.42320
n_iter = 3 J = 16746. max(relative change in state) = 71.630
n_iter = 4 J = 76.892 max(relative change in state) = 71.347
n_iter = 5 J = 76.486 max(relative change in state) = 0.11244E-01
n_iter = 6 J = 372.96 max(relative change in state) = 9.9179
n_iter = 7 J = 53.391 max(relative change in state) = 8.7327
n_iter = 8 J = 49.452 max(relative change in state) = 0.30239
n_iter = 9 J = 43.141 max(relative change in state) = 0.74608
n_iter = 10 J = 43.110 max(relative change in state) = 0.25568
n_iter = 11 J = 43.023 max(relative change in state) = 0.12759
n_iter = 12 J = 43.016 max(relative change in state) = 0.75272E-02
n_iter = 13 J = 42.915 max(relative change in state) = 0.76997E-01
n_iter = 14 J = 43.524 max(relative change in state) = 0.47670
n_iter = 15 J = 42.887 max(relative change in state) = 0.41171
n_iter = 16 J = 42.879 max(relative change in state) = 0.58047E-02
n_iter = 17 J = 42.767 max(relative change in state) = 0.10087
n_iter = 18 J = 43.014 max(relative change in state) = 0.34790
n_iter = 19 J = 42.726 max(relative change in state) = 0.28058
n_iter = 20 J = 42.710 max(relative change in state) = 0.14024E-01
n_iter = 21 J = 42.560 max(relative change in state) = 0.13914
n_iter = 22 J = 42.400 max(relative change in state) = 0.64642E-01
INFO (from ropp_1dvar_cost): Convergence assumed to be achieved as the cost function is increasing
This again confirms that MINROPP in the default configuration stops the iteration prematurely, mainly because it stops the iteration as soon as the cost function increases. I agree that this is meaningful criterion for stopping iterations, but only if the minmizer implements a reliable line search along the gradient as part of the minimisation step (which MINROPP apparently doesn't). Forcing the number of iterations to be at least 50 (e.g., using ecmwf_bangle_1dvar-03.cf), one can see that MINROPP is approaching the minimum, albeit rather slowly, and with multiple spikes in the cost function:
INFO (from ropp_1dvar_cost): Using absolute decrease of cost function and relative change
of state vector as additional convergence criteria.
n_iter = 1 J = 97.039 max(relative change in state) = -
n_iter = 2 J = 79.446 max(relative change in state) = 0.42320
n_iter = 3 J = 16746. max(relative change in state) = 71.630
n_iter = 4 J = 76.892 max(relative change in state) = 71.347
n_iter = 5 J = 76.486 max(relative change in state) = 0.11244E-01
n_iter = 6 J = 372.96 max(relative change in state) = 9.9179
n_iter = 7 J = 53.391 max(relative change in state) = 8.7327
n_iter = 8 J = 49.452 max(relative change in state) = 0.30239
n_iter = 9 J = 43.141 max(relative change in state) = 0.74608
n_iter = 10 J = 43.110 max(relative change in state) = 0.25568
n_iter = 11 J = 43.023 max(relative change in state) = 0.12759
n_iter = 12 J = 43.016 max(relative change in state) = 0.75272E-02
n_iter = 13 J = 42.915 max(relative change in state) = 0.76997E-01
n_iter = 14 J = 43.524 max(relative change in state) = 0.47670
n_iter = 15 J = 42.887 max(relative change in state) = 0.41171
n_iter = 16 J = 42.879 max(relative change in state) = 0.58047E-02
n_iter = 17 J = 42.767 max(relative change in state) = 0.10087
n_iter = 18 J = 43.014 max(relative change in state) = 0.34790
n_iter = 19 J = 42.726 max(relative change in state) = 0.28058
n_iter = 20 J = 42.710 max(relative change in state) = 0.14024E-01
n_iter = 21 J = 42.560 max(relative change in state) = 0.13914
n_iter = 22 J = 42.400 max(relative change in state) = 0.64642E-01
n_iter = 23 J = 188.86 max(relative change in state) = 6.7741
n_iter = 24 J = 42.325 max(relative change in state) = 6.6345
n_iter = 25 J = 42.317 max(relative change in state) = 0.25400E-02
n_iter = 26 J = 43.298 max(relative change in state) = 0.61042
n_iter = 27 J = 42.012 max(relative change in state) = 0.54511
n_iter = 28 J = 41.982 max(relative change in state) = 0.43726E-01
n_iter = 29 J = 41.951 max(relative change in state) = 0.80449E-01
n_iter = 30 J = 41.936 max(relative change in state) = 0.12898E-01
n_iter = 31 J = 41.765 max(relative change in state) = 0.11462
n_iter = 32 J = 10026. max(relative change in state) = 55.447
n_iter = 33 J = 41.752 max(relative change in state) = 55.395
n_iter = 34 J = 41.748 max(relative change in state) = 0.19056E-03
n_iter = 35 J = 1476.0 max(relative change in state) = 21.022
n_iter = 36 J = 41.556 max(relative change in state) = 20.884
n_iter = 37 J = 41.431 max(relative change in state) = 0.57102E-02
n_iter = 38 J = 57.723 max(relative change in state) = 2.4647
n_iter = 39 J = 36.069 max(relative change in state) = 2.2406
n_iter = 40 J = 35.672 max(relative change in state) = 0.17386
n_iter = 41 J = 35.431 max(relative change in state) = 0.25593
n_iter = 42 J = 35.399 max(relative change in state) = 0.10832E-01
n_iter = 43 J = 34.818 max(relative change in state) = 0.19488
n_iter = 44 J = 35.400 max(relative change in state) = 0.47172
n_iter = 45 J = 34.808 max(relative change in state) = 0.42144
n_iter = 46 J = 34.807 max(relative change in state) = 0.36675E-03
n_iter = 47 J = 34.437 max(relative change in state) = 0.23499
n_iter = 48 J = 38.018 max(relative change in state) = 1.1354
n_iter = 49 J = 34.405 max(relative change in state) = 1.0396
n_iter = 50 J = 34.403 max(relative change in state) = 0.99782E-03
INFO (from ropp_1dvar_solve): Minimization of cost function successfully finished (according to additional
convergence criteria). Number of required iterations: 50.
I was considering to modify the code to disable stopping the iteration in case of an increasing cost function, but found the code in MINROPP a bit convoluted; I therefore decided to stick with the LEVMARQ minimiser.
LEVMARQ
When looking into the code, I found that the LEVMARQ also stops as soon as the cost function starts to increase because of the main iteration is controlled by the statement (in line 177 of the file ropp_1dvar/common/ropp_1dvar_levmarq.f90)
DO WHILE(J <= J_min)
Replacing this with
DO WHILE(J <= 2.*J_min)
and reducing the convergence criteria from
conv_check_max_delta_state = 0.1 # State vector must change less than this * bg error
conv_check_max_delta_J = 0.1 # Cost function must change less than this
to
conv_check_max_delta_state = 0.0001 # State vector must change less than this * bg error
conv_check_max_delta_J = 0.0001 # Cost function must change less than this
results in the following iteration behaviour (ecmwf_bangle_1dvar-04.cf - note that this requires a modified version of the LEVMARQ minimiser, see above):
INFO (from ropp_qc_bgqc): Background quality control lets all bending angle values pass.
n_iter = 1 J = 97.039 max(relative change in state) = -
n_iter = 2 J = 32.400 max(relative change in state) = 0.13905
n_iter = 3 J = 32.382 max(relative change in state) = 0.16073
n_iter = 4 J = 32.378 max(relative change in state) = 0.12803
n_iter = 5 J = 32.376 max(relative change in state) = 0.12886
n_iter = 6 J = 32.378 max(relative change in state) = 0.12885
n_iter = 7 J = 32.416 max(relative change in state) = 0.12841
n_iter = 8 J = 32.482 max(relative change in state) = 0.98499E-01
n_iter = 9 J = 32.559 max(relative change in state) = 0.16935E-01
n_iter = 10 J = 32.593 max(relative change in state) = 0.80768E-03
n_iter = 11 J = 32.596 max(relative change in state) = 0.88798E-05
n_iter = 12 J = 32.596 max(relative change in state) = 0.88887E-07
INFO (from ropp_1dvar_levmarq): Convergence assumed to be achieved as the state vector did not change by more
than 0.10000E-03 relative to the assumed background errors for the last 2 iterations.
One may increase the minimum number of iterations required for convergence and will then find that additional iterations remain at a cost function value of 32.596. Note that this final cost function value is not the minimum of the cost function; that appears to be more around 32.376. The difference in this case is probably irrelevant in practice, but I still wonder why the LEVMARQ minimiser of ROPP is arriving at a false minimum if it clearly has been closer to the real one before. May that point towards an undiscovered issues in the calculation of the gradient/adjoint?
Other observations
- The last experiment requires a modification to the ROPP source code, because the minimizer loop in the released ROPP versions stops as soon as the cost function value increases. There is nothing in the output of the LEVMARQ scheme that makes the user aware, however; in case of MINROPP, the logging output tells the user the correct reason why the minimisation was terminated.
- All four sample scripts also run a bending angle 1DVar on a second test case (data/eum/first-tropical.nc), one of the first tropical occultations observed by Metop-C. All issues are found in this example as well.
Attachments (30)
Change history (59)
by , 7 years ago
| Attachment: | 1dvar-issues.tar.gz added |
|---|
comment:1 by , 7 years ago
The files to which Christian refers, including the README.me file that appears above, can be found in the attached 1dvar-issues.tar.gz file. Should you wish to find something, its contents are as follows:
unix_prompt> tar -ztvf 1dvar-issues.tar.gz drwxr-xr-x marq/staff 0 2019-01-27 23:30 1dvar-issues/ -rwxr-xr-x marq/staff 941 2019-01-22 14:42 1dvar-issues/run_1dvar-03 -rwxr-xr-x marq/staff 209 2019-01-26 22:13 1dvar-issues/._run_1dvar-04 -rwxr-xr-x marq/staff 947 2019-01-26 22:13 1dvar-issues/run_1dvar-04 -rwxr-xr-x marq/staff 210 2019-01-27 15:07 1dvar-issues/._run_1dvar-05 -rwxr-xr-x marq/staff 947 2019-01-27 15:07 1dvar-issues/run_1dvar-05 -rwxr-xr-x marq/staff 941 2019-01-22 13:36 1dvar-issues/run_1dvar-02 -rw-r--r-- marq/staff 13931 2019-01-22 13:34 1dvar-issues/ecmwf_bangle_1dvar-02.cf -rw-r--r-- marq/staff 214 2019-01-27 21:55 1dvar-issues/._ecmwf_bangle_1dvar-06.cf -rw-r--r-- marq/staff 13925 2019-01-27 21:55 1dvar-issues/ecmwf_bangle_1dvar-06.cf -rw-r--r-- marq/staff 13931 2019-01-22 14:42 1dvar-issues/ecmwf_bangle_1dvar-03.cf -rw-r--r-- marq/staff 16477 2019-01-23 13:09 1dvar-issues/README.md -rwxr-xr-x marq/staff 941 2019-01-22 11:27 1dvar-issues/run_1dvar-00 -rw-r--r-- marq/staff 13931 2019-01-23 12:52 1dvar-issues/ecmwf_bangle_1dvar-04.cf -rwxr-xr-x marq/staff 941 2019-01-22 11:32 1dvar-issues/run_1dvar-01 -rwxr-xr-x marq/staff 210 2019-01-27 20:53 1dvar-issues/._run_1dvar-06 -rwxr-xr-x marq/staff 947 2019-01-27 20:53 1dvar-issues/run_1dvar-06 -rw-r--r-- marq/staff 13931 2019-01-22 11:22 1dvar-issues/ecmwf_bangle_1dvar-00.cf -rw-r--r-- marq/staff 13931 2019-01-22 11:31 1dvar-issues/ecmwf_bangle_1dvar-01.cf -rw-r--r-- marq/staff 215 2019-01-27 16:44 1dvar-issues/._ecmwf_bangle_1dvar-05.cf -rw-r--r-- marq/staff 13931 2019-01-27 16:44 1dvar-issues/ecmwf_bangle_1dvar-05.cf drwxr-xr-x marq/staff 0 2019-01-22 08:59 1dvar-issues/data/ drwxr-xr-x marq/staff 0 2019-01-23 13:09 1dvar-issues/.idea/ -rw-r--r-- marq/staff 543 2019-01-22 11:27 1dvar-issues/.idea/1dvar-issues.iml -rw-r--r-- marq/staff 135 2019-01-22 11:24 1dvar-issues/.idea/encodings.xml drwxr-xr-x marq/staff 0 2019-01-22 11:27 1dvar-issues/.idea/libraries/ -rw-r--r-- marq/staff 8427 2019-01-23 13:09 1dvar-issues/.idea/workspace.xml -rw-r--r-- marq/staff 276 2019-01-22 11:24 1dvar-issues/.idea/modules.xml -rw-r--r-- marq/staff 288 2019-01-22 11:24 1dvar-issues/.idea/misc.xml -rw-r--r-- marq/staff 123 2019-01-22 11:27 1dvar-issues/.idea/libraries/R_User_Library.xml drwxr-xr-x marq/staff 0 2019-01-22 08:59 1dvar-issues/data/ecmwf/ drwxr-xr-x marq/staff 0 2019-01-22 08:59 1dvar-issues/data/metop-c/ drwxr-xr-x marq/staff 0 2019-01-22 08:59 1dvar-issues/data/errors/ -rw-r--r-- marq/staff 248004 2019-01-22 08:56 1dvar-issues/data/errors/ropp_ob_bangle_error_corr_247L.nc -rw-r--r-- marq/staff 309168 2019-01-22 08:57 1dvar-issues/data/errors/ropp_bg_ses_ecmwf_error_corr_L137.nc -rw-r--r-- marq/staff 39072 2019-01-22 08:51 1dvar-issues/data/metop-c/first.nc -rw-r--r-- marq/staff 39072 2019-01-22 08:51 1dvar-issues/data/metop-c/first-tropical.nc -rw-r--r-- marq/staff 76596 2019-01-22 08:55 1dvar-issues/data/ecmwf/GRAS_1B_M03_20181113100752Z_20181113100945Z_N_C_20181113121522Z_G22_NN.fw.nc -rw-r--r-- marq/staff 76596 2019-01-22 08:55 1dvar-issues/data/ecmwf/GRAS_1B_M03_20181113101119Z_20181113101335Z_N_C_20181113121522Z_G05_NN.fw.nc
comment:2 by , 7 years ago
Chris's description:
"There are five scripts and five configuration scripts; the one with the -00 at the end of the name is identical to the default configuration file in the ropp v9.0 distribution apart from the settings for the background and observation errors. Each script simply runs both sample cases. The README.md describes the results in terms of the first profile, but the same issues can also be seen for the second profile.
The bending angle profiles are in data/metop-c, and the corresponding forward modelled ECMWF background profiles in data/ecmwf; the latter still indicates the formal names of the occultations. Error files are in data/error; I simply copied the files of the same name from the ropp v9.0 source code distribution again. Note that for running the last version, you need to patch the loop controlling the LEVMARQ minimizer; details are in the README.md."
comment:3 by , 7 years ago
Joe Nielsen (DMI) confirmed that he sees the same behaviour:
Dear Christian
I can briefly confirm that I can reproduce your results, except for that fact that I get slightly different numerical output. The difference can be rationalized since I have modified the ROPP 1D-Var since the last ROPP update.
The main point is that I also see an increase in the cost function for both for MINROPP and LEVMARQ like you do, and I can see in our own log-files that it happens from time to time. I never paid attention to that before I am afraid. So I acknowledge that there is nothing in the code to prevent that, and the fixes that I have made recently do not improve on that particular issue.
comment:4 by , 7 years ago
Chris replied:
Personally, I'm not overly concerned that the cost functions goes slightly up - as long as it goes down later on. My one point was that as far as I understand, the bending angle 1DVars both use an increase in the cost function as a reason to stop - which I think they shouldn't if it is ok to have an occasional glitch in the minimizer (i.e., not really minimising). There is an interaction with the minimum_number_of_iterations parameter (or however it is called); my gut feeling is that this interaction is also slightly different for MINROPP and LEVMARQ, but I didn't check that thoroughly, to be honest.
The other thing - do you also see the increase of the cost function before LEVMARQ arrives at its "solution" in the last run? I was concerned about that because it actually went through a smaller cost function value before (in step 5), but then finished at a slightly higher value later on. As if the gradient would become zero at the minimum, but slightly elsewhere...
comment:5 by , 7 years ago
Joe commented:
Hi Chris, focussing on levmarq and ignoring minropp for now
Yes I can confirm that behaviour (dumped output after DO WHILE(J <= 2.*J_min) modification at end of mail). I never really looked into the minimizers code before. I suppose levmarq is a pragmatic approach that works pretty good for our purpose. The convergence criterion being enforced here,
MAXVAL(delta_state) < config%conv_check_max_delta_state
does not really ensure that the gradient is zero (just close). As long as neither of the convergence criteria are met the algorithm would allow the cost function to gradually increase, had it not been for the DO WHILE(J <= J_min) criterion. Can that lead to an increase of the cost function while the gradient is deceasing?
I tried to simply print out the gradient dJ_dx in each step. To my surprise it does not change at all after step 5 where the costfunction starts to rise. This is also where the algorithm would normally exit, so it is a consequence of the algorithm being corrupted by DO WHILE(J <= 2.*J_min). But looking at the code I cannot see how the gradient could EVER be calculated in the marq = .TRUE. situation?
The algorithm is coded such that it runs (approximately) Newtonian until the cost function rises. Then "marq" is switched on and the gradient is frozen for the remaining iterations. They, however, are never realized since J>J_min forces the iteration to exit anyway. How could that ever work? Now it seems to me that we have been running almost Newtonian all the time...
I guess that I am confusing myself now. We need a fresh view on this.
My 1D-Var output: I tried to print out lambda between each iteration, it increases dramatically while the state vector slows down.
---------------------------------------------------------------------
ROPP Bending Angle 1D-Var
---------------------------------------------------------------------
INFO (from ropp_1dvar_bangle): Reading configuration file ecmwf_bangle_1dvar-04.cf.
INFO (from ropp_1dvar_bangle): Reading observation data for profile 1 from the file ./data/metop-c/first.nc.
INFO (from ropp_1dvar_bangle): Reading background data for profile 1 from the file
./data/ecmwf/GRAS_1B_M03_20181113100752Z_20181113100945Z_N_C_20181113121522Z_G22_NN.fw.nc.
INFO (from ropp_qc_cutoff): 33 points rejected for being above maximum impact height of 50.0 km.
INFO (from ropp_qc_bgqc): Background quality control lets all bending angle values pass.
1.000000000000000E-005
n_iter = 1 J = 96.809 max(relative change in state) = -
1.000000000000000E-006
n_iter = 2 J = 32.342 max(relative change in state) = 0.13047
1.000000000000000E-007
n_iter = 3 J = 32.316 max(relative change in state) = 0.15385
1.000000000000000E-008
n_iter = 4 J = 32.313 max(relative change in state) = 0.12655
1.000000000000000E-009
n_iter = 5 J = 32.309 max(relative change in state) = 0.12624
1.000000000000000E-007
n_iter = 6 J = 32.312 max(relative change in state) = 0.12624
1.000000000000000E-005
n_iter = 7 J = 32.350 max(relative change in state) = 0.12579
1.000000000000000E-003
n_iter = 8 J = 32.415 max(relative change in state) = 0.96576E-01
0.100000000000000
n_iter = 9 J = 32.490 max(relative change in state) = 0.16884E-01
10.0000000000000
n_iter = 10 J = 32.523 max(relative change in state) = 0.13641E-02
1000.00000000000
n_iter = 11 J = 32.526 max(relative change in state) = 0.15004E-04
100000.000000000
n_iter = 12 J = 32.526 max(relative change in state) = 0.15019E-06
INFO (from ropp_1dvar_levmarq): Convergence assumed to be achieved as the state vector did not change by more than 0.10000E-03
relative to the assumed background errors for the last 2 iterations.
comment:6 by , 7 years ago
Last word for now to Chris.
Hi Joe,
thanks for looking into it; at least I know I'm not completely wrong. Your description of what you see finally caused me to read up on the Levenberg-Marquardt (LM) algorithm; I fact I always ran away from that (and actually used to have canned minimisers rather than writing one myself when doing my own 1DVars many years ago).
So what I understood from e.g. the Numerical Recipes (sec 15.5 in the second edition) or the book by Rodgers (2000, p.92) is that the LM algorithm works like this:
- For a given value of the damping parameter (lambda), calculate an increment dx to the state vector;
- Calculate the value of the cost function J (or Chi2) for an updated state vector x + dx;
- If J increases as the result of a step, increase the damping parameter, keep the (previous) state vector x (i.e, do not update it with dx), and try again;
- If J decreases as a result of the step, update the state vector x with the increment dx, and decrease the damping parameter for the next step.
Thus, the current ROPP implementation doesn't implement the LM; or worse, it implements it wrongly:
- If the cost function increases during the minimisation, the iteration stops in the original version (due to the condition in the header of the
whileloop) rather than updating lambda; thus, an update of the damping parameter is actually never performed in practice in the original code. The minimizer instead solely performs in the steepest decent with the initial value of lambda, not implementing the update of the damping parameter which is at the core of the LM algorithm. In the worst case, it might stop iterating prematurely before the minimum of the cost function is found. - When disabling the iteration stop at the first increase of the cost function during the iteration, there are two more issues:
- It does not stick with the previous state vector when increasing the damping parameter, but instead uses an updated one;
- It does not update the cost function’s gradient and Hessian accordingly.
Because of the latter, when allowing updates to the damping parameter, the current implementation drifts away from the true minimum as seen in the last experiment I ran. With increasing values of lambda, the step size along the (incorrect) gradient becomes smaller and smaller, so that the iteration finally halts for very large values of the damping parameter.
I refactored the code a bit to implement the LM correctly; the version compatible to the Numerical Recipes is in the attached file ropp_1dvar_levmarq_nr.f90. The handling of the damping parameter updates as described in the Numerical Recipes is a simplified version of the original algorithms; and there seem to have been refinements over the year. As far as I understand, one nowadays seems to use “trust region” based methods which really is just a pompous name for a slightly more refined update strategy. A good summary are the Technical Report from Nielsen (1999; link see below – is the family name an accident?), also described in some Lecture Notes by Madsen et al. (2004). I’ve implemented these ones in the other two Fortran files attached, ropp_1dvar_levmarq_tr1.f90 for eq. (2.4), and ropp_1dvar_levmarq_tr2.f90 for eq. (2.5) in the Nielsen report. Note that there might be bugs; I ran the code over my sample case, but didn’t do any more testing. Probably one should also add some scaling of the variables (that’s described in Madsen et al., and even the original paper by Marquardt in 1963), but I didn’t have the time over the weekend. Maybe I can do later this week...
Anyway, this is what I get out when running them with similar settings as for the last experiment in my previous mail:
- NumRec: J = 32.365, 11 iterations (26 forward model / gradient evaluations) - Trust region 1: J = 32.360, 11 iterations (31 forward model / gradient evaluations) - Trust region 2: J = 32.370, 12 iterations (13 forward model / gradient evaluations)
The original implementation bailed out at J = 32.378, and ended up at J = 32.596 (after 11 iterations) when updates to the damping parameter were allowed. So all three implementations get closer to the minimum, but with different computational effort. There are several parameters to tune, but at least all do better in this particular example than the current ROPP version. For the above numbers, I disabled the cost function convergence check; I still might have a bug in there as it is cancelling the iteration too early. I’ll try to have a look into that... I also attached another tar file; there are two new configuration files for testing (plus the old ones). The file ecmwf_bangle_1dvar-06.cf produces the results above, while the file ending with -05.cf forces the iteration to run much longer in order to see how it evolves. Not that cost function values do increase in between; that is why second variant of the trust region update tries to smoothly vary the damping parameter, and it mostly works.
I’m not sure how to proceed. I’d personally argue that the current ROPP implementation doesn’t provide an LM minimiser; it’s just steepest descent with premature stopping. I believe it should be fixed. I’ll probably spent a little bit of time in adding the scaling and then using that in our 1DVar for bending angles until you in the SAF have decided what to do about this.
Oh. I didn’t touch the code for refractivity at all. I wondered why there are two different functions for the bending angle and the refractivity minimiser which are nearly identical (apart from the calls to the respective forward models); I’d rather have a more generic minimiser that is used in both 1DVar variants. But well – there’s always a history, of course...
comment:8 by , 7 years ago
So it all looks quite bad, really. Chris says he believes it should be fixed, and I agree. Note that there is a longstanding ROPP 'whenever' ticket (#234) to look at the discrepancy between the minROPP and LevMarq minimisers in ROPP; perhaps the time is now ripe for a thorough re-examination of both.
comment:9 by , 7 years ago
Here are some final comments from Joe.
Thank you for this Chris. We must discuss in the team what to do. Clearly we cannot have MinROPP as the default with the malfunctions you found. And in my opinion we must replace LM, starting from the new version that you have provided (I have not had time to look at it yet). We think that the current ROPP LM his working sufficiently good (apparently to some extent by luck), so there is not an immediate crisis with the products. But the code is wrong, and I believe that we must find resources to fix it and test the fix. We shall discuss this in relation to the other tasks at hand.
I agree.
comment:10 by , 7 years ago
And some thoughts on this from Chris.
That makes a lot of sense… I’d also believe that as long as you’re using the Levenberg-Marquardt version you’re probably not creating major issues for refractivity; I remember from many years ago that it was mostly the bending angle 1DVar that tended to be a bit difficult for the minimiser. Maybe you should nevertheless check to be sure, anyway ...
comment:11 by , 7 years ago
| Cc: | added |
|---|---|
| Priority: | normal → major |
With Joe's approval, add him in cc and raise priority to 'major'.
comment:12 by , 7 years ago
Hi,
I just attached three newer versions of the updated Levenberg-Marquardt minimisers - when I processed larger numbers of profiles, I found that the I had a bug in the first version that updated a variable wrongly, and in some cases, it happened that the damping parameter grew beyond all bounds, in effect stopping the convergence. Both are now fixed.
Chris
comment:13 by , 7 years ago
Thanks Chris. For the record, at the ROPP-CG meeting on 6/6/2019 we agreed this fix was a high priority for inclusion in ROPP10.0.
We also agreed two related actions:
- Joe - to carry out similar investigation using refractivity
- Ian - to make LevMarq the default minimiser in ROPP
by , 6 years ago
| Attachment: | fwarrick_results.txt added |
|---|
Reproducing Chris' results at the Met Office
comment:14 by , 6 years ago
See attached file 'fwarrick_results.txt'
I have re-run Chris' tests at the Met Office using ROPP 9.0
Most tests returned identical results except run_1dvar-02 and run_1dvar-03 though the results are similar - J decreases but with occasional spikes then gives up before reaching the minimum J seen in other tests.
Also I assumed 'mu' should be 'lambda' on line 402 of ropp_1dvar_levmarq_nr.2.f90
comment:15 by , 6 years ago
The first attempt at incorporating ropp_1dvar_levmarq_nr.2.f90 into bangle and refrac halves of ROPP-10's ropp_1dvar_levmarq.f90 has been made at r6207. (I think mu should be lambda_max, incidentally.)
The only one of ropp_1dvar's automatic make tests that uses LevMarq is test_1dvar_iono.sh. The new results are different enough from the reference values, generated by the earlier code, that they fail the (rather tight) comparison tests:
Running t_1dvar_iono_bangle (1DVAR L1 and L2) ...
----------------------------------------------------------------------
ROPP 1DVAR File Comparison Tool
----------------------------------------------------------------------
INFO (from ropp_1dvar_compare): Comparing anl20090401_000329_M02_2030337800_N0007_YYYY_iono.nc and ../data/anl20090401_000329_M02_2030337800_N0007_YYYY_iono_reference.nc:
the results of running test t_1dvar_iono_bangle (1DVAR L1 and L2)
ERROR (from ropp_io_fields_compare): Profile 1 Lev1b%bangle_L1 values ARE significantly different: |diff| = 1.84905E-06 > 1.00000E-06
ERROR (from ropp_io_fields_compare): Profile 1 Lev1b%bangle_L2 values ARE significantly different: |diff| = 1.84326E-06 > 1.00000E-06
ERROR (from ropp_io_fields_compare): Profile 1 Lev2c%press_sfc values values ARE significantly different: |diff| = 2.31934E-03 > 1.00000E-06
ERROR (from ropp_io_fields_compare): Profile 1 Lev2c%ne_max values values ARE significantly different: |diff| = 1.71934E+09 > 1.00000E-06
ERROR (from ropp_io_fields_compare): Profile 1 Lev2c%h_peak values values ARE significantly different: |diff| = 8.24812E+02 > 1.00000E-06
ERROR (from ropp_io_fields_compare): Profile 1 Lev2c%h_width values values ARE significantly different: |diff| = 2.72500E+01 > 1.00000E-06
INFO (from ropp_1dvar_compare): 6 differences exist in profile 1
INFO (from ropp_1dvar_compare): 6 elements of anl20090401_000329_M02_2030337800_N0007_YYYY_iono.nc and ../data/anl20090401_000329_M02_2030337800_N0007_YYYY_iono_reference.nc differ significantly
****************************
********** *FAIL* **********
****************************
... examine t_1dvar_iono_bangle.log for details
The iteration records are as follows.
ROPP9.1:
n_iter = 1 J = 239.02 max(relative change in state) = -
n_iter = 2 J = 67.763 max(relative change in state) = 0.36367
n_iter = 3 J = 46.930 max(relative change in state) = 0.14259
n_iter = 4 J = 44.530 max(relative change in state) = 0.28843E-01
n_iter = 5 J = 44.529 max(relative change in state) = 0.90156E-02
INFO (from ropp_1dvar_levmarq): Convergence assumed to be achieved as the state vector did not change by more
than 0.10000 relative to the assumed background errors for the last 2 iterations.
ROPP10.0:
n_iter = 0 J = 210.01 max(relative change in state) = -
n_iter = 1 J = 54.377 max(relative change in state) = 858.30
n_iter = 2 J = 45.498 max(relative change in state) = 0.62841
n_iter = 3 J = 44.760 max(relative change in state) = 0.18211
n_iter = 4 J = 44.758 max(relative change in state) = 0.33700E-01
n_iter = 5 J = 44.757 max(relative change in state) = 0.14134E-01
INFO (from ropp_1dvar_levmarq_bangle): Convergence assumed to be achieved as the state vector did not change by more
than 0.10000 relative to the assumed background errors for the last 2 iterations.
INFO (from ropp_1dvar_levmarq_bangle): Finished after 5 iterations (5 forward model / gradient evaluations).
Here's a picture of the change in bangle_L1 between ROPP 9.1 and 10.0:
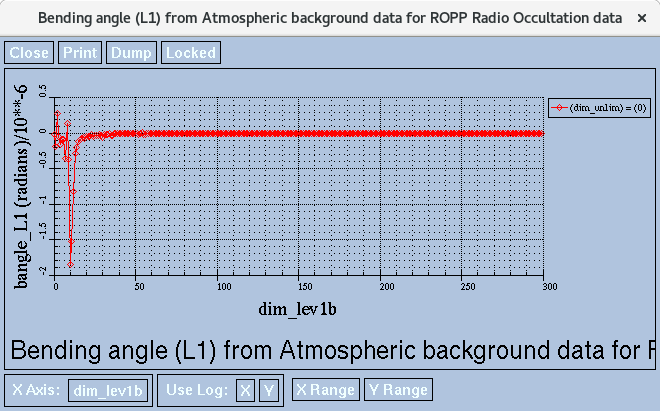
All these look like the sort of differences to be expected, so it seems safe to update the reference file. This has been done at r6208.
comment:16 by , 6 years ago
| Cc: | added |
|---|
When we change the configuration files to make the other tests use LevMarq rather than minROPP, then, not surprisingly, all tests fail the comparison tests due to the huge differences between the results of the two minimisation schemes. More worryingly, it fails one of the standard tests, test_1dvar_GRAS_refrac.sh:
n_iter = 0 J = 40.261 max(relative change in state) = -
n_iter = 1 J = 35.373 max(relative change in state) = 823.02
n_iter = 1 J = 35.492 lambda -> 0.10000E-03
n_iter = 1 J = 35.496 lambda -> 0.10000E-02
n_iter = 1 J = 35.498 lambda -> 0.10000E-01
n_iter = 1 J = 35.499 lambda -> 0.10000
n_iter = 1 J = 35.504 lambda -> 1.0000
n_iter = 1 J = 35.494 lambda -> 10.000
n_iter = 1 J = 35.409 lambda -> 100.00
n_iter = 1 J = 35.377 lambda -> 1000.0
n_iter = 1 J = 35.373 lambda -> 10000.
... some time later ...
n_iter = 1 J = 35.373 lambda -> 0.10000+292
n_iter = 1 J = 35.373 lambda -> 0.10000+293
n_iter = 1 J = 35.373 lambda -> 0.10000+294
which then gives a floating point overflow.
The reason is that n_iter is not incremented when lambda is being inflated, and so it never breaks out of the
DO WHILE (n_iter < n_iter_max)
loop.
We can avoid the overflow by adding a
IF (ABS(lambda) > lambda_max) THEN
WRITE(ch_str, '(g15.5)') lambda_max
ch_str = ADJUSTL(ch_str)
CALL message(msg_cont, '')
CALL message(msg_info, &
'Levenberg-Marquardt parameter exceeded max (=' // TRIM(ch_str) // &
'); convergence is unlikely.\n ' // &
'Check convergence parameters; conv_check_max_delta_J might ' // &
'be too demanding.\n')
EXIT
END IF
test in the lambda-inflating part of the code (Sec 1.8.1 and 2.8.1).
This change has been committed at r6212.
But it doesn't address the root of the problem, which is that the cost function only approaches the earlier, lower value asymptotically from above, so that it never gets below the value that it must (J_last in the code) before it is judged to have converged. The history of J and lambda are shown here:
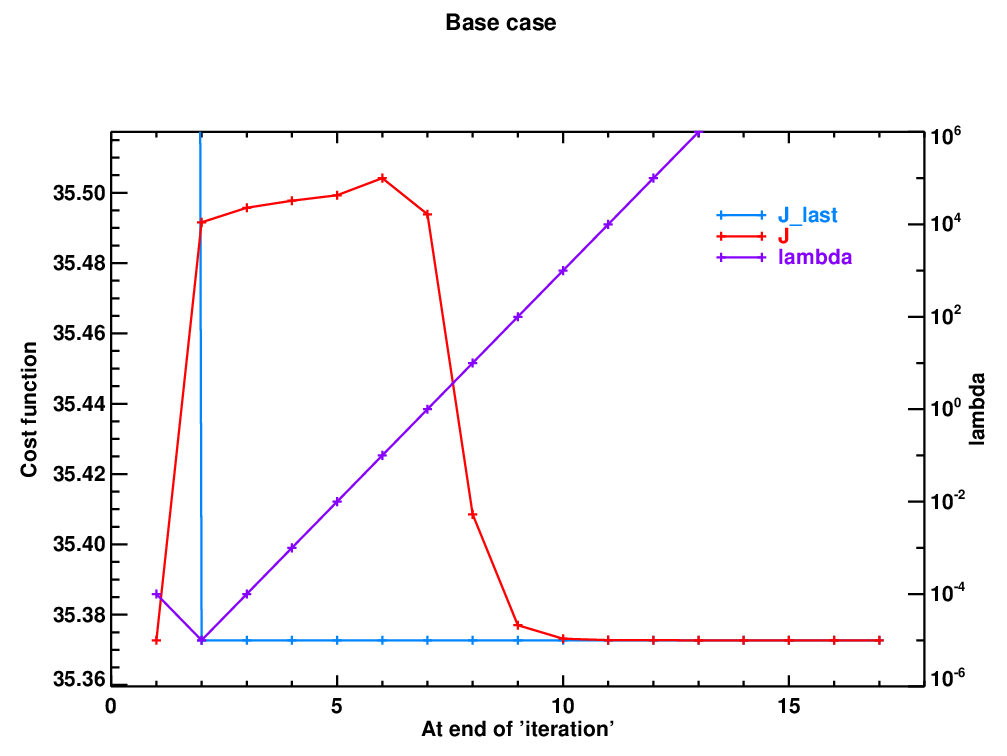 You can see that the revised LM scheme does pretty well by the end of iteration 1, but that it doesn't know when to stop, and 'accidentally' increases
You can see that the revised LM scheme does pretty well by the end of iteration 1, but that it doesn't know when to stop, and 'accidentally' increases J. The scheme therefore steadily increases lambda, to make it more like a steepest descents algorithm. This starts to reduce J after about 4 or 5 attempts, but it never gets below the value at the end of iteration 1, and is therefore never deemed to converge. (In fact, J-J(at iter 1) keeps reducing by a factor of 10 (= the multiplier of lambda) every 'iteration' in this regime.) Without the 'if lambda > lambda_max then bail out' fix described above, the exponential growth of lambda eventually leads to a floating point overflow.
I don't really understand this behaviour - or, rather, I don't understand why it isn't more widespread. We are basically reducing the step length by a factor of 10 (in the high lambda regime) every attempted iteration, so to me it's not surprising that the cost function only asymptotically approaches its target. Why doesn't this happen more often? (All the standard bending angle tests, and most[*] of the other refractivity tests all run OK. ([*] 6 out of the 10 GRAS refrac profiles; all 5 of the COSMIC refrac profiles.))
One possible fix is to relax the strict test for failure to reduce the cost function, from
IF ( J >= J_last ) THEN ! Keep previous state vector, increase lambda, repeat
to
IF ( J >= (J_last + config%conv_check_max_delta_state) ) THEN ! Keep previous state vector, increase lambda, repeat
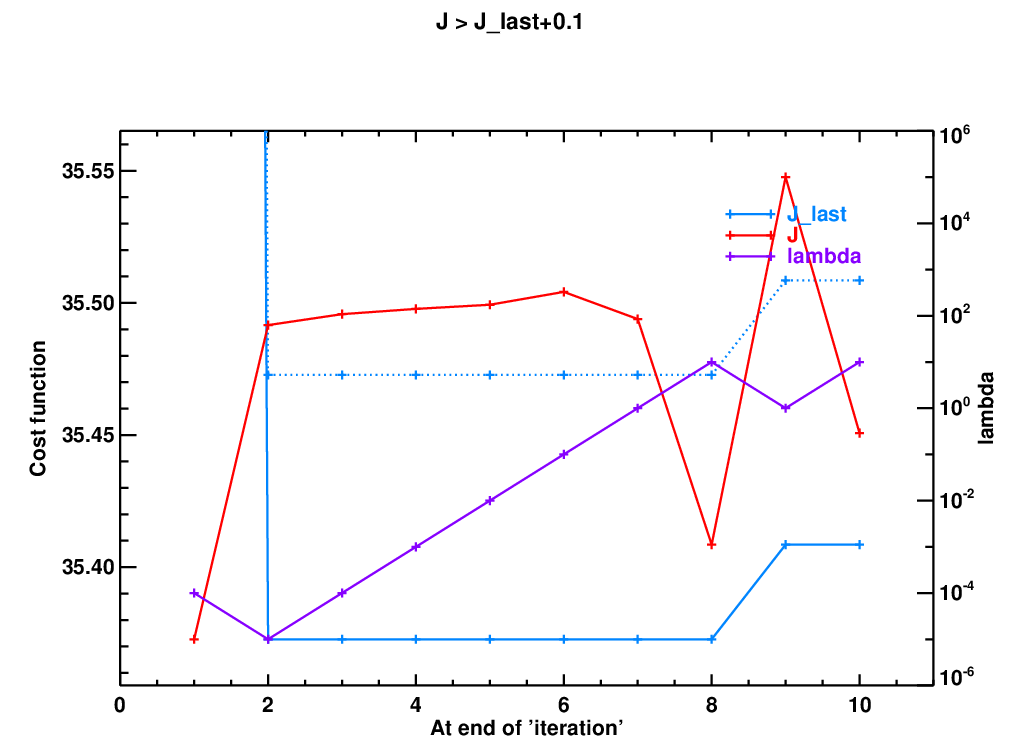
where config%conv_check_max_delta_state = 0.1 by default. This seems to be in accord with the advice on the LM algorithm in Numerical Recipes, which says one should stop iterating when J decreases by 'a negligible amount'. When we do this, all the refractivity profiles converge fairly quickly to what appear at first sight to be reasonable solutions. This conclusion needs to be tested further. Be that as it may, the convergence picture corresponding to the one above is now
It shows that when J falls within the config%conv_check_max_delta_state envelope of J_last, lambda starts decreasing and we rapidly reach a solution (because the state vector is not changing significantly):
n_iter = 0 J = 40.261 max(relative change in state) = -
n_iter = 1 J = 35.373 max(relative change in state) = 823.02
n_iter = 1 J = 35.492 lambda -> 0.10000E-03
n_iter = 1 J = 35.496 lambda -> 0.10000E-02
n_iter = 1 J = 35.498 lambda -> 0.10000E-01
n_iter = 1 J = 35.499 lambda -> 0.10000
n_iter = 1 J = 35.504 lambda -> 1.0000
n_iter = 1 J = 35.494 lambda -> 10.000
n_iter = 2 J = 35.409 max(relative change in state) = 0.32174E-01
n_iter = 2 J = 35.548 lambda -> 10.000
n_iter = 3 J = 35.451 max(relative change in state) = 0.30794E-01
INFO (from ropp_1dvar_levmarq_refrac): Convergence assumed to be achieved as the state vector did not change by more
than 0.10000 relative to the assumed background errors for the last 2 iterations.
INFO (from ropp_1dvar_levmarq_refrac): Finished after 3 iterations (10 forward model / gradient evaluations).
I don't know whether this fudge is acceptable: it's not really in the spirit of the pure Levenberg-Marquardt algorithm. On the other hand, we have to do something to get it to work in practice.
Anyway, this change has been committed at r6213, and uploaded to this ticket as ropp_1dvar_levmarq.f90.r6213.
comment:17 by , 6 years ago
Aargh! I said
IF ( J >= (J_last + config%conv_check_max_delta_state)
when I meant
IF ( J >= (J_last + config%conv_check_max_delta_J)
Fortunately, they both default to 0.1, so no harm done. Fix this at r6217.
comment:18 by , 5 years ago
Joe Nielsen at DMI tested the refractivity code. He reports:
Hi Ian, I tested the new Levenberg Marquart implementation on one day of Metop data, 2016-01-01, (1299 profiles). I used the background and atm files from ROM SAF CDR1.0. The baseline is just the current DMI trunk ROM SAF 1dvar applied on 60 levels. I tested this code:
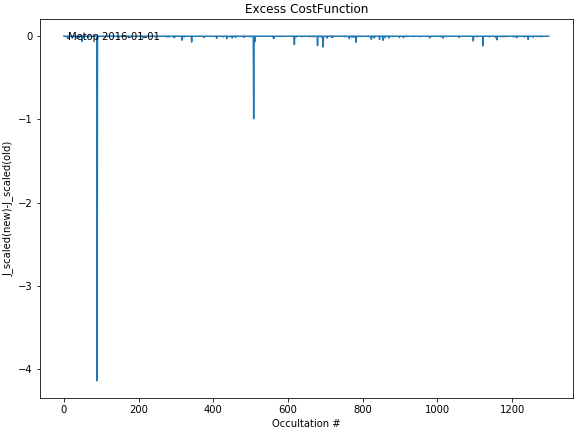
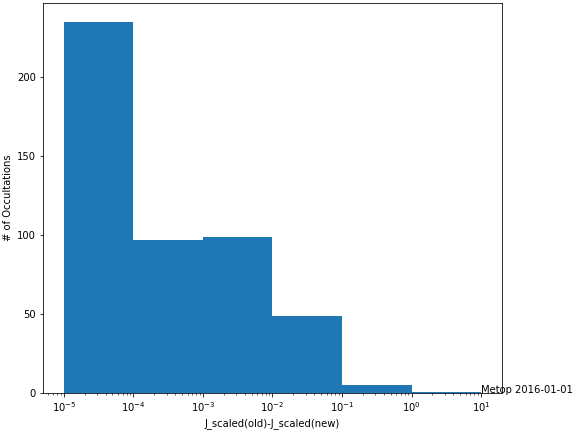
The improvement seems to work very good! The solution found with previous LevMarq implementation was not optimal (for once the word "optimal" can be used in its literal sense). J_scaled.png shows the decrease of the cost function (compared to the old solution).
1150 of the occultations show a drop in the cost function, most of them tiny, as seen in J_scaled_hist.
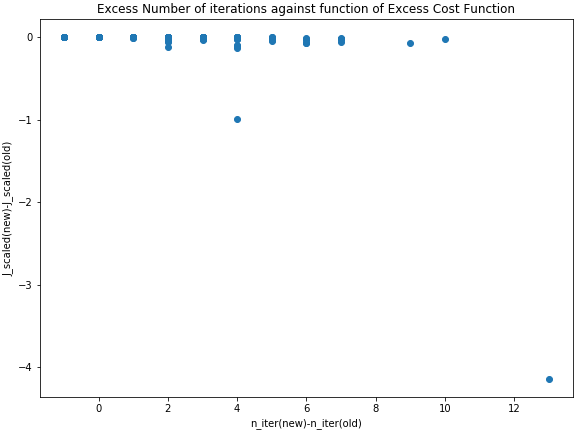
J_n_scatter.png shows the drop in cost function against the increased number of iterations. As expected, the new LevMarq will occasionally run a little further and find a better solution.
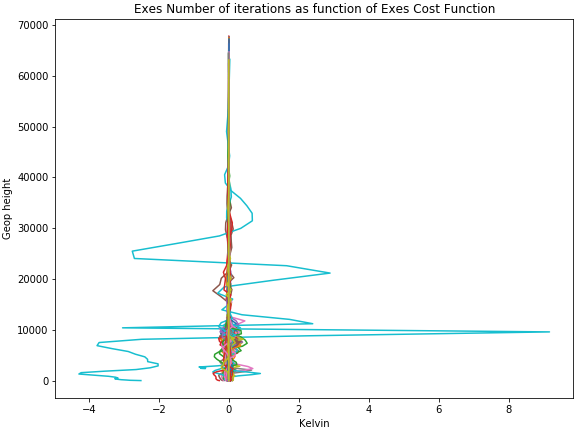
All good, but there are two occultations where the cost function is substantially lowered, which of course worries me. The temperature difference in the extreme case is more than 9 K at 10000 m in the worst case (see temperature plot NewLevMarqtemperature.png).
Fortunately, in this particular occultation, the refractivity was non-nominal in CDR v1-0. In the other case, where the \delta J_scaled is close to -1 the profile was declared nominal. However in that case the max temperature difference is below 0.1 K. In conclusion it behaves as we expected, it is a clear improvement, but it does not undermine the trust in CDR v1.0 dramatically. We cannot not rule out that there are very sporadic cases in the CDR v1.0 where the 1D-Var solution is significantly off and still has passed the QC. There is not much to do about that now I guess. Finally, I am really grateful that you have fixed the bug (and that Chris pointed it out)! Thanks a lot joe
comment:19 by , 5 years ago
I replied
Many thanks for doing this. I'm glad the new code is working as expected - that is, in a generally beneficial way. Thanks to Chris for his hard work in putting that together. Personally, I don't think two bogies in 1300 profiles is too much to worry about, especially as one of them was picked off by the nominality flag. Given the significant impact of the changes that Chris saw on the Metop-C profiles, which originally prompted his investigation, are you surprised that the changes don't have a bigger effect? I'm a little confused by the histogram of J_scaled(old)-J_scaled(new) plotted with a log x-axis. I can see the point that most of the time the change in cost function is very small, but it does of course prevent you displaying the stats in the ~150 cases when J(old) </= J(new), which might perhaps be suggestive. I'm not sure I have fixed a 'bug', if you're referring to the loosening of the condition that J(this_iter) must be strictly less than J(previous_iters) before we reduce lambda and start homing in on the solution. If anything, I've introduced one, since it's not part of the formal LevMarq algorithm. But Numerical Recipes says we should stop iterating when J decreases by a negligible amount, and this gives us a way of getting there. And I found that the example 1dvar refractivity test in ROPP got stuck in a regime where J asymptotically approached, but never matched, its earlier minimum, and therefore just kept increasing lambda until we got a floating point overflow. So we had to do something. As you've shown, it seems to work OK in practice.
comment:20 by , 5 years ago
Chris chipped in:
Well, I observed big difficulties of the old implementation in bending angle 1DVars, not in the refractivity version. The reason Joe looked into this in more detail was to make sure that our expectation that refractivity likely isn't affected is indeed correct. Chris.
comment:21 by , 5 years ago
Joe replied
To your suggestion Ian; there are indeed some (38) cases where the cost function
increase. I hadn't even noticed. These are very tiny values. It is easier to
just print them explicitly than to plot them:
ind2=np.where(((ds.J_scaled-db.J_scaled)>0).values)
(ds-db).J_scaled[ind2[0][:]]
Out [149]:
<xarray.DataArray 'J_scaled' (dim_unlim: 38)>
array([1.192093e-07, 7.152557e-07, 4.768372e-07, 5.960464e-07, 9.775162e-06,
4.768372e-07, 8.344650e-07, 3.576279e-07, 4.768372e-07, 2.980232e-08,
9.536743e-07, 2.980232e-07, 2.980232e-08, 7.450581e-08, 1.490116e-07,
3.159046e-06, 5.960464e-08, 9.536743e-07, 2.384186e-07, 1.490116e-07,
9.238720e-07, 2.384186e-07, 1.192093e-07, 2.980232e-08, 5.960464e-07,
2.384186e-07, 2.205372e-06, 2.980232e-08, 5.960464e-08, 9.536743e-07,
1.072884e-06, 5.960464e-08, 2.980232e-08, 5.960464e-08, 6.824732e-06,
1.192093e-07, 2.980232e-08, 2.980232e-08], dtype=float32)
A lot of them has been achieved with one less iteration than with the old
LevMarq:
(ds-db).n_iter[ind2[0][:]]
Out [150]:
<xarray.DataArray 'n_iter' (dim_unlim: 38)> array([-1., 0., -1., -1., -1., 0., 0., -1., -1., 0., -1., -1., -1., 0.,
-1., -1., -1., -1., -1., -1., -1., 0., -1., -1., 0., -1., -1., -1.,
-1., 0., 0., -1., -1., -1., -1., -1., -1., -1.], dtype=float32)
Regarding your question, which Chris already commented on. We observe, what was
expected, that refractivity 1D-Var is easier for the minimizer than
bending-angle 1D-Var, and that the "truncated" Levenberg Marquart luckily did a
reasonable job. It would have been an unpleasant surprise otherwise!
joe
comment:22 by , 5 years ago
comment:23 by , 5 years ago
Joe said
I do not quite understand why you say that the negative changes in J-scaled are not interesting? I think they are the interesting examples, with values up to some order of magnitude as the cost function itself, while the positive changes of 10-7 are uninteresting... Let me see, we are not defining the axis direction in the same way, right? joe
comment:24 by , 5 years ago
I said (famous last words, I hope)
OK, I mean the ones where the cost function is bigger in the new code: the ones in my histogram. They don't seem to show any interesting pattern.
comment:25 by , 5 years ago
| Milestone: | 10.0 → 11.0 |
|---|
I haven't had time to make LevMarq the default - that would require the reference datasets for the core tests and test folder to be updated. So shift this ticket to ROPP-11.0. Users can easily pick their preferred solver with an option in the configuration file.
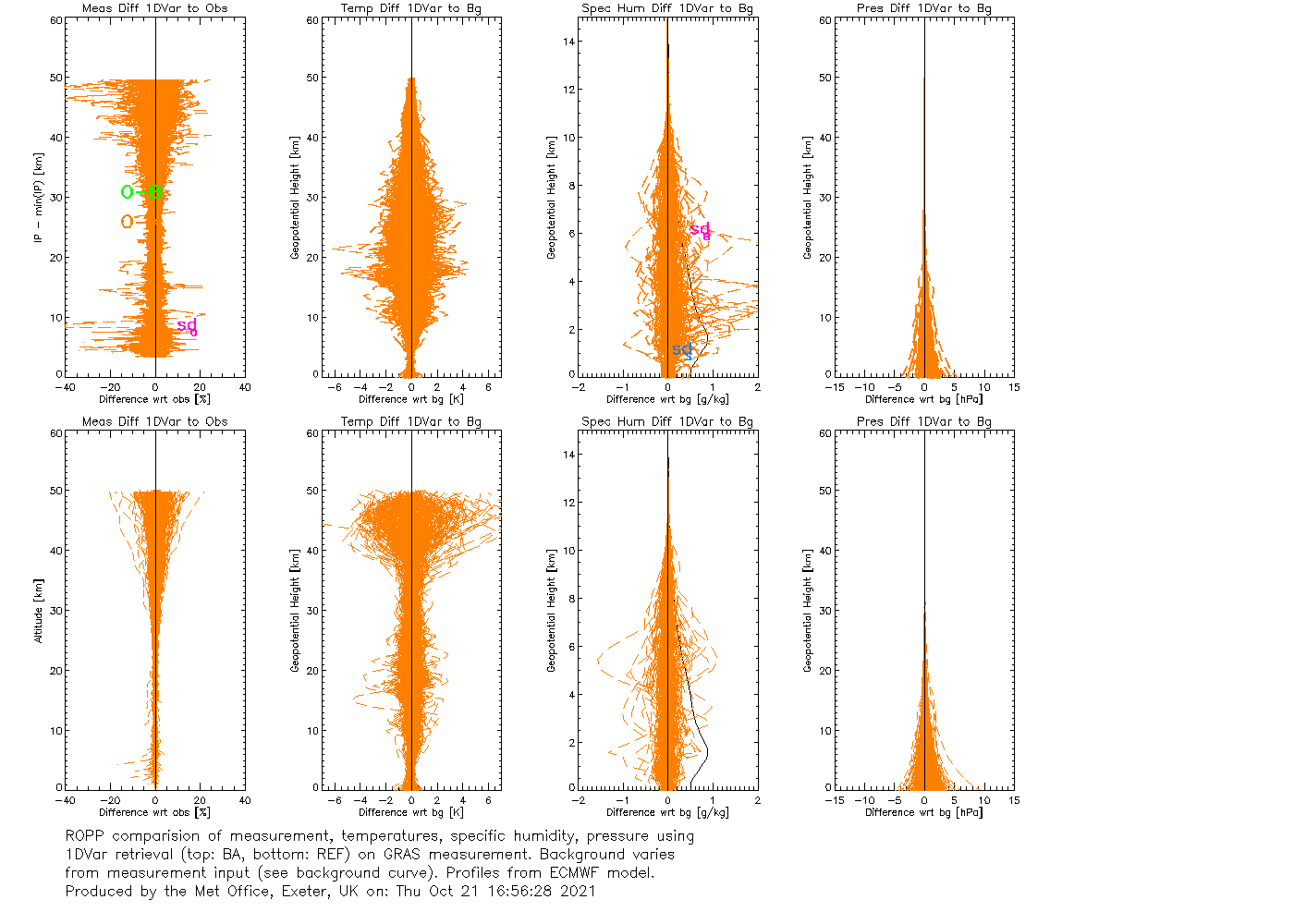
by , 4 years ago
| Attachment: | IT-1DVAR-03_gfortran_linux_ROPP10.png added |
|---|
IT-1DVAR-03_gfortran_linux_ROPP10.png
by , 4 years ago
| Attachment: | IT-1DVAR-05_gfortran_linux_ROPP10.png added |
|---|
IT-1DVAR-05_gfortran_linux_ROPP10.png
by , 4 years ago
| Attachment: | IT-1DVAR-OP_gfortran_linux_ROPP10.png added |
|---|
IT-1DVAR-OP_gfortran_linux_ROPP10.png
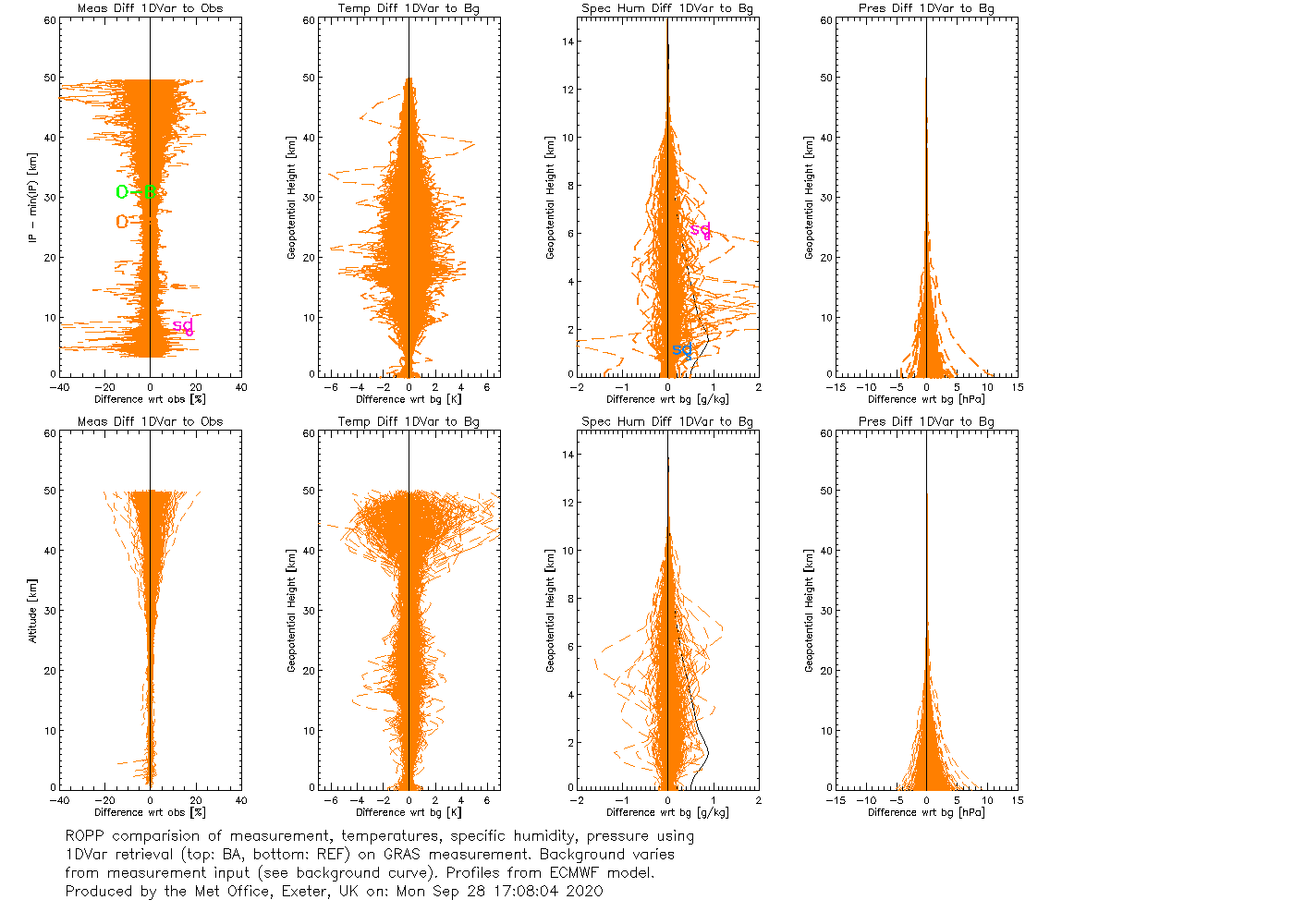
by , 4 years ago
| Attachment: | IT-1DVAR-03_gfortran_linux_ROPP11.png added |
|---|
IT-1DVAR-03_gfortran_linux_ROPP11.png
by , 4 years ago
| Attachment: | IT-1DVAR-05_gfortran_linux_ROPP11.png added |
|---|
IT-1DVAR-05_gfortran_linux_ROPP11.png
by , 4 years ago
| Attachment: | IT-1DVAR-OP_gfortran_linux_ROPP11.png added |
|---|
IT-1DVAR-OP_gfortran_linux_ROPP11.png
comment:26 by , 4 years ago
LevMarq has been made the default minimiser in ROPP at r6943 and r6946. This change will be incorporated in ROPP-11.0.
I haven't done any particularly extensive investigations of the impact of this change, because I suspect that most users will run ropp_1dvar with a configuration file, and will therefore have made a conscious choice of the minimiser that they wish to use by means of the (poorly named) minropp_method option in that file, which will override any default. But some of the 1DVAR tests in the test folder are run without a configuration file, and therefore the minimiser that they use has changed in going from ROPP-10.0 to ROPP-11.0. What impact does this change have on these tests?
Reassuringly, not much. Generally speaking, LevMarq converges to a slightly lower cost function in fewer iterations, although it needs more CPU time to do it. Here's a bit more detail.
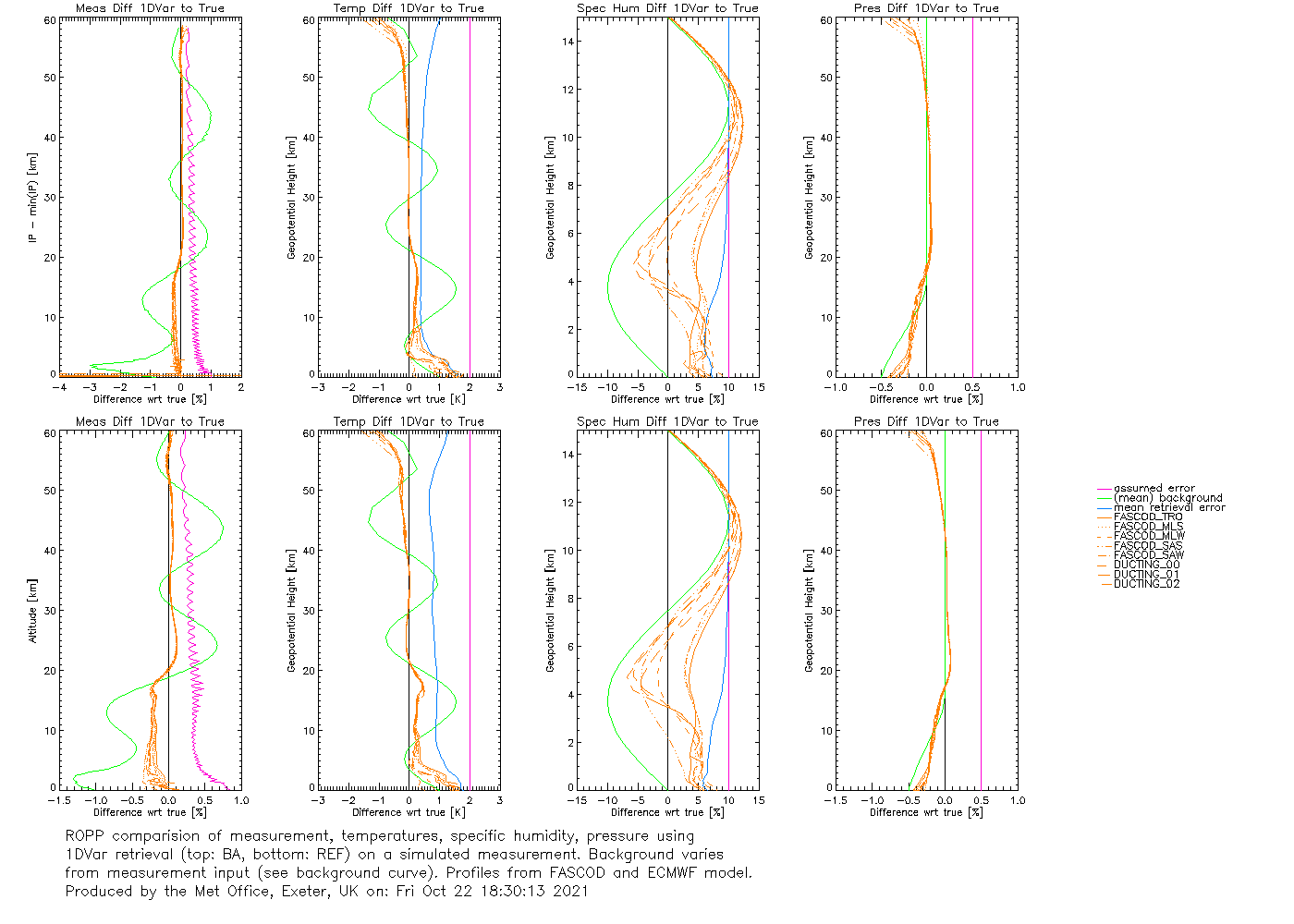
IT-1DVAR-03
(5 FASCOD + 3 'DUCTING' profiles are forward modelled to bangle and refrac. Sinusoidal noise is added to create pseudo obs, which are then used in a 1dvar retrieval. The test passes if OmA is at least 40% smaller than OmB.)
ROPP-11 on first profile (for bangle):
n_iter = 0 J = 206.08 max(relative change in state) = -
n_iter = 1 J = 11.942 max(relative change in state) = 847.61
n_iter = 2 J = 8.1870 max(relative change in state) = 0.26167
n_iter = 3 J = 8.1826 max(relative change in state) = 0.59874E-02
n_iter = 4 J = 8.1826 max(relative change in state) = 0.15115E-02
INFO (from ropp_1dvar_levmarq_bangle): Convergence assumed to be achieved as the state vector did not change by more
than 0.10000 relative to the assumed background errors for the last 2 iterations.
INFO (from ropp_1dvar_levmarq_bangle): Finished after 4 iterations (4 forward model / gradient evaluations).
.
.
.
Average processing time [s]: 2.726
(cpu times for processing all 8 profiles, twice)
cf
ROPP-10 on first profile (for bangle):
INFO (from ropp_1dvar_cost): Using absolute decrease of cost function and relative change
of state vector as additional convergence criteria.
n_iter = 1 J = 206.08 max(relative change in state) = -
n_iter = 2 J = 119.99 max(relative change in state) = 0.34101
n_iter = 3 J = 63.160 max(relative change in state) = 0.55012
n_iter = 4 J = 50.929 max(relative change in state) = 0.18262
n_iter = 5 J = 42.314 max(relative change in state) = 0.12822
n_iter = 6 J = 32.378 max(relative change in state) = 0.20368
n_iter = 7 J = 27.748 max(relative change in state) = 0.16416
n_iter = 8 J = 23.770 max(relative change in state) = 0.92587E-01
n_iter = 9 J = 19.958 max(relative change in state) = 0.14694
n_iter = 10 J = 16.197 max(relative change in state) = 0.20782
n_iter = 11 J = 14.819 max(relative change in state) = 0.11343
n_iter = 12 J = 13.724 max(relative change in state) = 0.30200E-01
n_iter = 13 J = 13.173 max(relative change in state) = 0.19778E-01
INFO (from ropp_1dvar_cost): Convergence assumed to be achieved as the state vector did not change by more
than 0.10000 relative to the assumed background errors for the last 2 iterations.
INFO (from ropp_1dvar_solve): Minimization of cost function successfully finished (according to additional
convergence criteria). Number of required iterations: 13.
.
.
.
Average processing time [s]: 1.980
(cpu times for processing all 8 profiles, twice)
Not much in it - in fact the differences are small enough that the LM code still passes the test folder. I hadn't expected that. The cpu time differences are interesting. They show that even though LevMarq needs fewer forward model/gradient evaluations than minROPP (3.2 cf 9.2 on average), the cost of doing each one is so much higher that the overall cpu time is about 40% higher for LevMarq. Perhaps this is because it doesn't do pre-conditioning, whereas minROPP does?
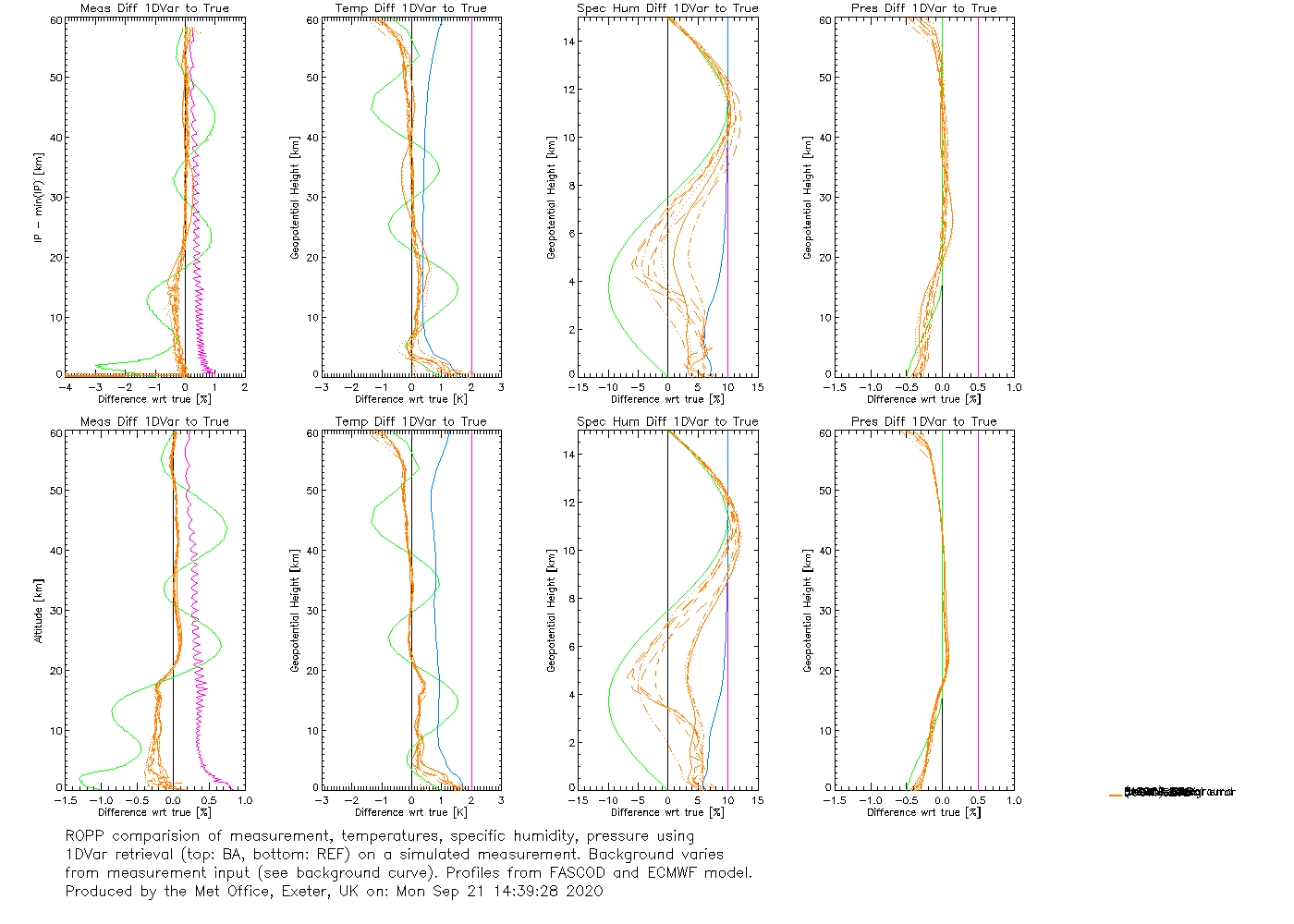
IT-1DVAR-05
(1DVAR retrievals of 10 GRAS bangle & refrac profiles, with ECMWF backgrounds. Test passes if OmA < OmB. Repeated for new interpolation scheme.)
Same sort of story, e.g.:
ROPP-11 on first profile (for refrac):
n_iter = 0 J = 57.369 max(relative change in state) = -
n_iter = 1 J = 29.130 max(relative change in state) = 822.57
n_iter = 2 J = 29.091 max(relative change in state) = 0.13758
n_iter = 3 J = 29.087 max(relative change in state) = 0.10097E-01
INFO (from ropp_1dvar_levmarq_refrac): Convergence assumed to be achieved as the cost function did not change by more
than 0.10000 for the last 2 iterations.
INFO (from ropp_1dvar_levmarq_refrac): Finished after 3 iterations (3 forward model / gradient evaluations).
.
.
.
Average processing time [s]: 4.058
(cpu times for processing all 10 profiles, 4 times)
cf
ROPP-10 on first profile (for refrac):
INFO (from ropp_1dvar_cost): Using absolute decrease of cost function and relative change
of state vector as additional convergence criterium.
n_iter = 1 J = 57.369 max(relative change in state) = -
n_iter = 2 J = 53.348 max(relative change in state) = 0.31163
n_iter = 3 J = 47.030 max(relative change in state) = 1.0136
n_iter = 4 J = 50.313 max(relative change in state) = 0.69203
n_iter = 5 J = 45.967 max(relative change in state) = 0.74136
INFO (from ropp_1dvar_cost): Convergence assumed to be achieved as the cost function is increasing
INFO (from ropp_1dvar_cost): Minimization of cost function successfully finished (according to additional
convergence criteria). Number of required iterations: 6.
.
.
.
Average processing time [s]: 2.696
(cpu times for processing all 10 profiles, 4 times)
In this case, LevMarq needs an average of 3.4 forward model / gradient evaluations per profile, while minROPP needs 8.9. LevMarq still needs 50% more cpu time.
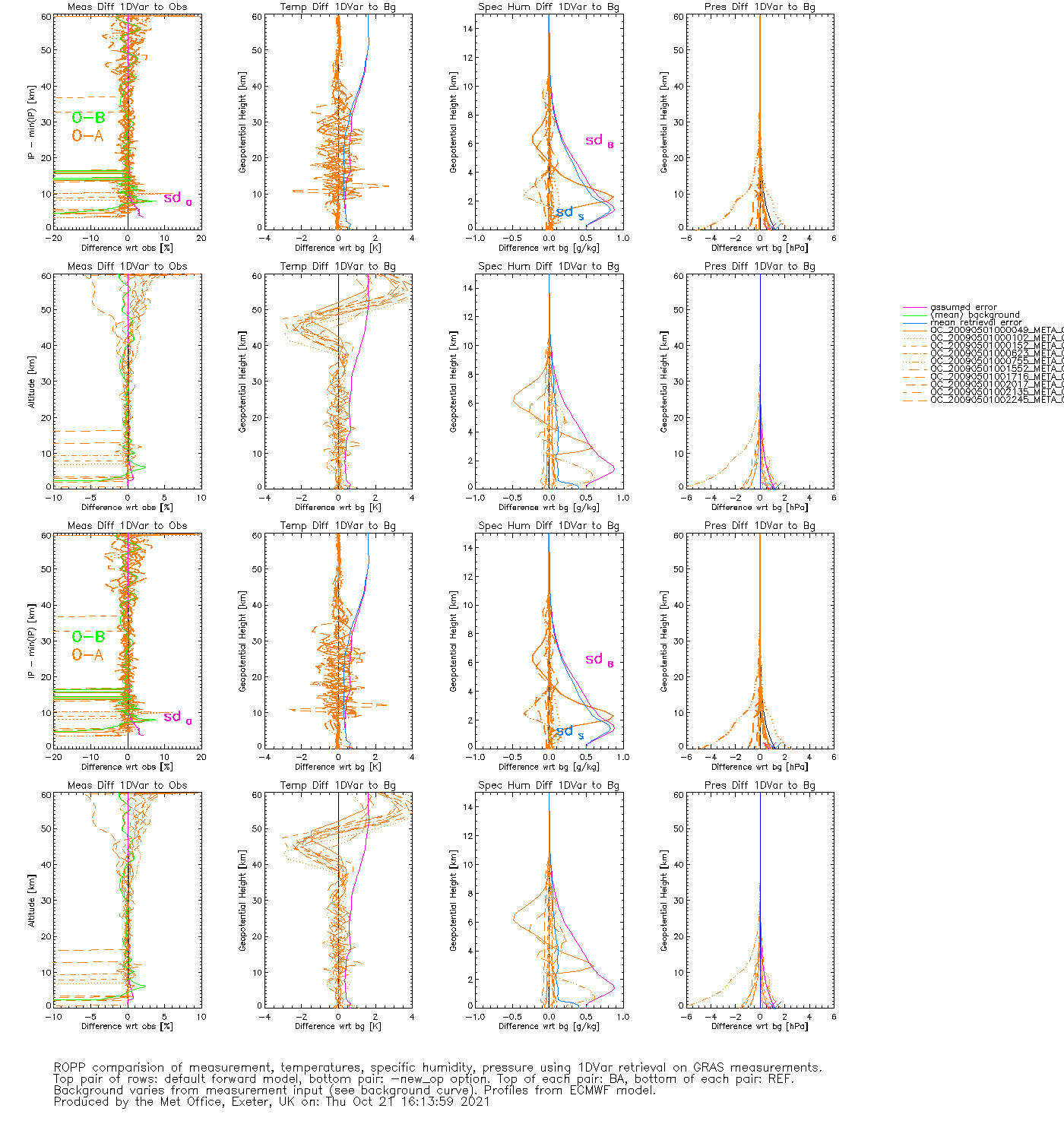
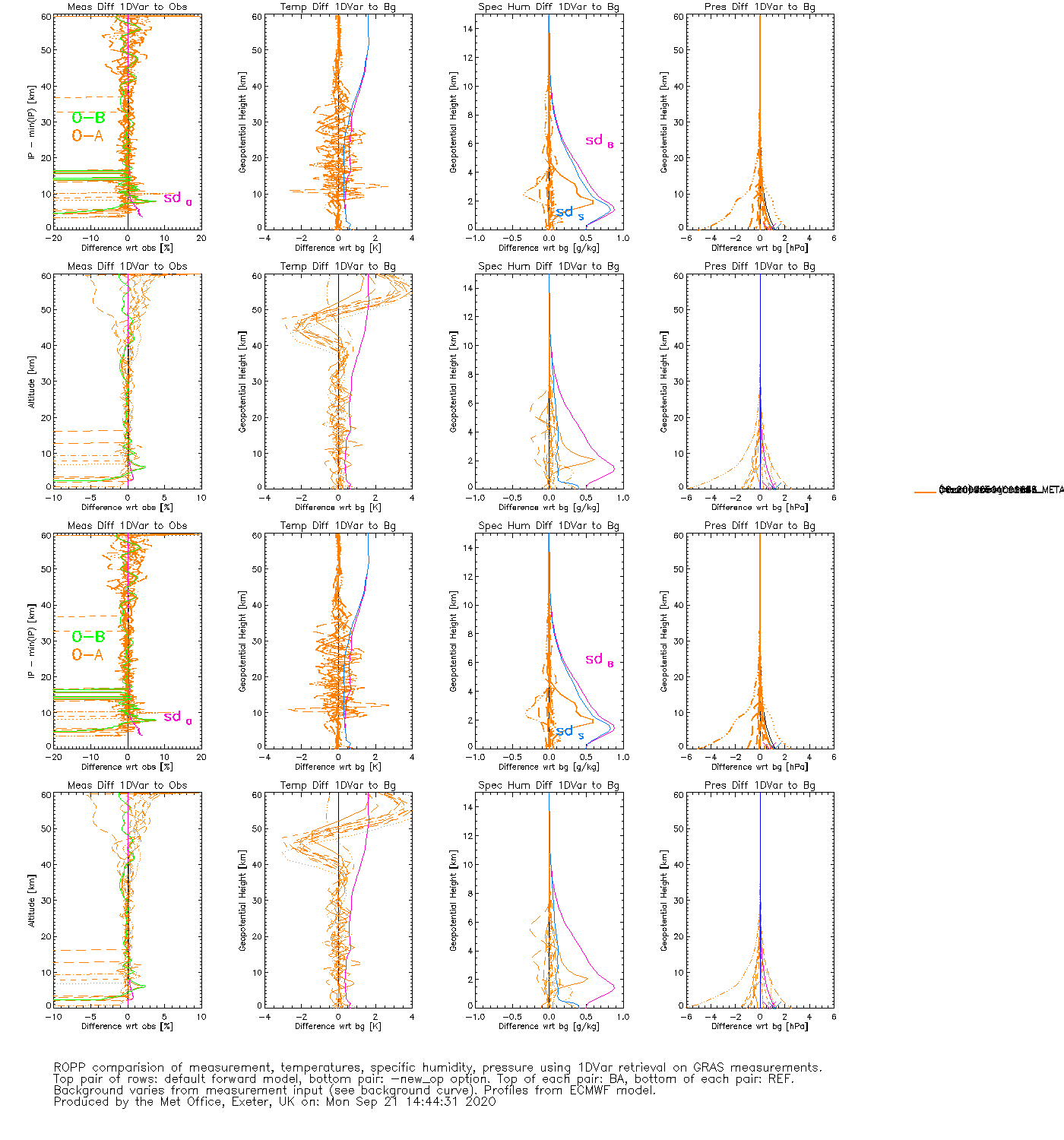
IT-1DVAR-OP
(1DVAR retrievals of 625 GRAS bangle & refrac profiles, with ECMWF backgrounds. Test passes if OmA < OmB.)
Same again, e.g.:
ROPP-11 on first profile (for bangle):
n_iter = 0 J = 176.73 max(relative change in state) = -
n_iter = 1 J = 98.622 max(relative change in state) = 1010.7
n_iter = 2 J = 98.577 max(relative change in state) = 0.12666
n_iter = 3 J = 98.577 max(relative change in state) = 0.25168E-02
INFO (from ropp_1dvar_levmarq_bangle): Convergence assumed to be achieved as the cost function did not change by more
than 0.10000 for the last 2 iterations.
INFO (from ropp_1dvar_levmarq_bangle): Finished after 3 iterations (3 forward model / gradient evaluations).
.
.
.
Average processing time [s]: 208.034
(cpu times for processing all 625 profiles, twice)
cf
ROPP-10 on first profile (for bangle):
INFO (from ropp_1dvar_cost): Using absolute decrease of cost function and relative change
of state vector as additional convergence criteria.
n_iter = 1 J = 176.73 max(relative change in state) = -
n_iter = 2 J = 110.06 max(relative change in state) = 3.5523
n_iter = 3 J = 100.24 max(relative change in state) = 1.4568
n_iter = 4 J = 99.548 max(relative change in state) = 0.54384
n_iter = 5 J = 99.040 max(relative change in state) = 0.37328
n_iter = 6 J = 98.927 max(relative change in state) = 0.76776E-01
n_iter = 7 J = 98.848 max(relative change in state) = 0.87230E-01
INFO (from ropp_1dvar_cost): Convergence assumed to be achieved as the state vector did not change by more
than 0.10000 relative to the assumed background errors for the last 2 iterations.
INFO (from ropp_1dvar_solve): Minimization of cost function successfully finished (according to additional
convergence criteria). Number of required iterations: 7.
.
.
.
Average processing time [s]: 151.684
(cpu times for processing all 625 profiles, twice)
This time, LevMarq needs 3.5 forward model/gradient evaluations per profile, while minROPP needs 8.0 iterations per profile, but uses ~ 30% more cpu time overall.
It's not clear from this, very limited, testing that the extra cpu cost of LevMarq buys any better results. But they're not any worse either, and the results of the early part of this ticket show that minROPP can behave very strangely in some circumstances, so a change of the ROPP default solver is still desirable.
by , 4 years ago
| Attachment: | IT-1DVAR-03_gfortran_linux_ROPP10.html added |
|---|
IT-1DVAR-03_gfortran_linux_ROPP10.html
by , 4 years ago
| Attachment: | IT-1DVAR-05_gfortran_linux_ROPP10.html added |
|---|
IT-1DVAR-05_gfortran_linux_ROPP10.html
by , 4 years ago
| Attachment: | IT-1DVAR-OP_gfortran_linux_ROPP10.html added |
|---|
IT-1DVAR-OP_gfortran_linux_ROPP10.html
by , 4 years ago
| Attachment: | IT-1DVAR-03_gfortran_linux_ROPP11.html added |
|---|
IT-1DVAR-03_gfortran_linux_ROPP11.html
by , 4 years ago
| Attachment: | IT-1DVAR-05_gfortran_linux_ROPP11.html added |
|---|
IT-1DVAR-05_gfortran_linux_ROPP11.html
by , 4 years ago
| Attachment: | IT-1DVAR-OP_gfortran_linux_ROPP11.html added |
|---|
IT-1DVAR-OP_gfortran_linux_ROPP11.html
comment:27 by , 4 years ago
Joe comments:
Thank you Ian. I am not so concerned about CPU time. Anyway I am not sure whether preconditioning would reduce the number of iterations of LevMarq further. But can you remind me why preconditioning is used in the minROPP test and not in LevMarq? I assume it is because someone has thought it through and concluded that it is not necessary. joe
I have no idea - the decision was taken long before I joined the SAF. Preconditioning isn't mentioned in GSR 6, which describes the LevMarq scheme. It is mentioned in GSR 3, which describes the minROPP scheme, but not with the usual meaning. The ROPP 1DVAR user guide is equally quiet on the question.
For the record, the new L2-L1 1dvar retrieval scheme, which Sean and I have developed, uses preconditioning with the LevMarq scheme, but in this case the state vector contains elements that can differ in magnitude by ~ 1014, so preconditioning is perhaps more likely to be useful/needed.
comment:28 by , 4 years ago
To summarise this (all results for ifort16, bangle and refrac combined):
IT-1DVAR-03 (8 FASCOD+DUCTING profiles)
| <n_iter> | <2J/m> | <CPU per prof> (sec) | |
| minROPP | 9.3 | 0.067 | 0.18 |
| LevMarq | 3.2 | 0.060 | 0.24 |
IT-1DVAR-05 (10 GRAS & ECMWF profs, old & new interp schemes)
| <n_iter> | <2J/m> | <CPU per prof> (sec) | |
| minROPP | 9.1 | 0.77 | 0.19 |
| LevMarq | 3.4 | 0.75 | 0.27 |
IT-1DVAR-OP (625 GRAS & ECMWF profs)
| <n_iter> | <2J/m> | <CPU per prof> (sec) | |
| minROPP | 8.6 | 0.91 | 0.19 |
| LevMarq | 3.7 | 0.91 | 0.25 |
So, roughly speaking, minROPP and LevMarq have similar performances on these tests (as measured by solution 2J/m). LevMarq takes around 50% more cpu time, but minROPP needs 2-3 times as many iterations.
comment:29 by , 4 years ago
| Resolution: | → fixed |
|---|---|
| Status: | new → closed |
This change has been incorporated in ROPP-11.0, so closing ticket as "done".

1dvar-issues.tar.gz